【数IA三角比】円に内接する四角形の対角線の長さを求める(千葉大2019第1問)
AB=5,BC=4,CD=4,DA=2
とする。また,対角線 AC と BD の交点を P とおく。
(1) 三角形 APB の外接円の半径を $R_1$,三角形 APD の外接円の半径を $R_2$ とするとき,$\cfrac{R_1}{R_2}$ の値を求めよ。
(2) AC の長さを求めよ。
外接円の半径
(1) 三角形 APB の外接円の半径を $R_1$,三角形 APD の外接円の半径を $R_2$ とするとき,$\cfrac{R_1}{R_2}$ の値を求めよ。
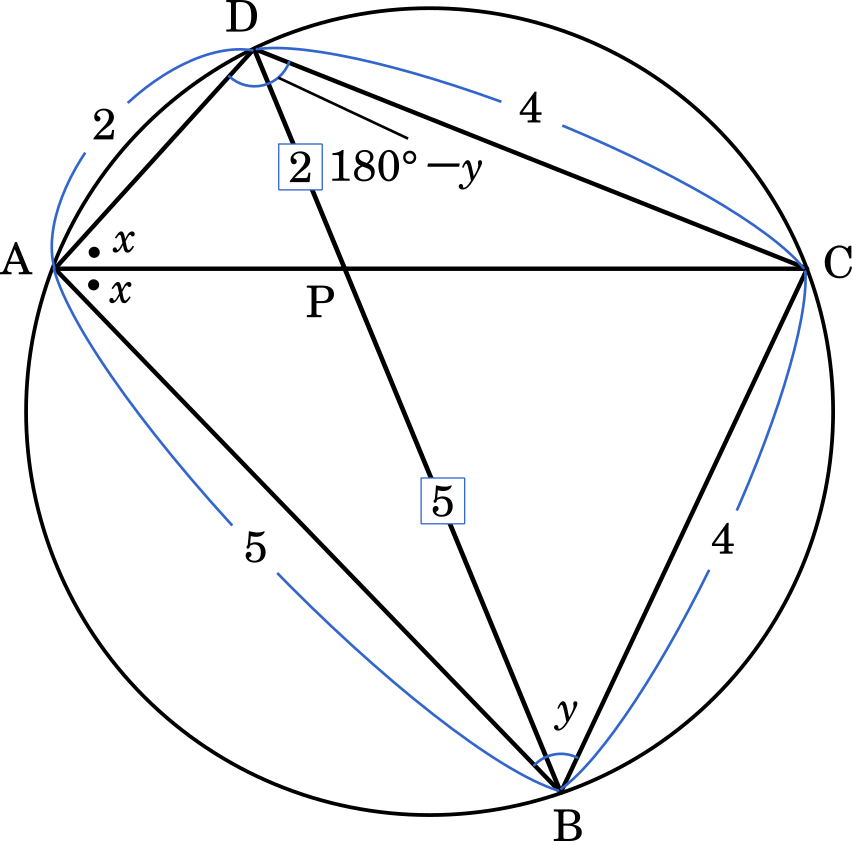
BC=CD=4 より,∠BAC=∠CAD が成り立ちます。
そうすると △ABD において,角の二等分線の性質より BP : DP = 5 :2 が成り立ちます。
ここから,外接円の半径を求めましょう。
正弦定理
△ABC の外接円の半径を $R$ とすると,次が成り立つ。
$\cfrac{a}{\text{sin}A}=\cfrac{b}{\text{sin}B}=\cfrac{c}{\text{sin}C}=2R$
$R_1$ と $R_2$ の比を求めるなら,辺の比である 5:2 をそのまま用いることができます。
∠BAC=∠CAD=$x$ とすると
$\cfrac{5}{\sin x}=2R_1$
$\cfrac{2}{\sin x}=2R_2$
よって
$\cfrac{R_1}{R_2}=\cfrac{5}{2}$ (答え)
余弦定理を利用する
(2) AC の長さを求めよ。
ここは余弦定理を利用しましょう。
円に内接する四角形の性質から
∠ABC+∠ADC=180°
が成り立ちます。
∠ABC=$y$ とすると,∠ADC=$180\degree-y$ となります。
このとき,$\cos$ は
$\cos(180\degree-y)=-\cos y$
となります。
これを利用して
△ABC について,余弦定理より
$\text{AC}^2=5^2+4^2-2\cdot5\cdot4\cos y$ ・・・①
△ADC について
$\text{AC}^2=2^2+4^2-2\cdot2\cdot4\cos(180\degree-y)$
$\text{AC}^2=2^2+4^2+2\cdot2\cdot4\cos y$ ・・・②
それぞれの式を整理すると
$\text{AC}^2=41-40\cos y$ ・・・①’
$\text{AC}^2=20+16\cos y$ ・・・②’
①’×2+②’×5
$\begin{aligned}&2\text{AC}^2&=&82-80\cos y\\+)&5\text{AC}^2&=&100+80\cos y\\\hline&7\text{AC}^2&=&182\end{aligned}$
$\text{AC}^2=26$
$\text{AC}=\sqrt{26}$ (答え)
SNSでシェア