【数III】fn(x)とgn(x)で値を交換する数列／tanが実数全体を表すことを利用する問題（千葉大2021第9問）

数学的帰納法

等式の形を見ると，$f$ の値が分かると $g$ の値が分かり，$g$ の値が分かると $f$ の値が分かるという関係になっています。

問題文のような漸化式を証明したいのなら数学的帰納法を用いればよいのですが，仮定の式を 2 つおいて考えるところに注意しましょう。

$\{f_{n+1}(x)\}’=(n+1)g_n(x)$，$\{g_{n+1}(x)\}’=-(n+1)f_n(x)$ ・・・（＊）

[I] $n=1$ のとき

$\{f_2(x)\}’=\{f_1(x)+xg_1(x)\}’$
$=\{x+x\}’=2x$
$=2g_1(x)$

$\{g_2(x)\}’=\{g_1(x)-xf_1(x)\}’$
$=\{1-x^2\}’=-2x$
$=-2f_1(x)$

よって，$n=1$ のとき，（＊）は成り立つ。

[II] $n=k$ のとき（＊）が成り立つと仮定して，$n=k+1$ とすると

$\{f_{k+2}(x)\}’=\{f_{k+1}(x)+xg_{k+1}(x)\}’$
$=\{f_{k+1}(x)\}’+\{xg_{k+1}(x)\}’$

$\{xg_{k+1}(x)\}’$ はかけ算の微分なので公式を使います。

$=\{f_{k+1}(x)\}’+(x)’g_{k+1}(x)+x\{g_{k+1}(x)\}’$

（＊）が成り立つと仮定しているので，これを代入します。
$=(k+1)g_k(x)+g_{k+1}(x)+x\{-(k+1)f_k(x)\}$

問題文の条件より $g_{n+1}(x)=g_n(x)-xf_n(x)$ だったので，これを用いて

$=(k+1)g_k(x)+g_k(x)-xf_k(x)+x\{-(k+1)f_k(x)\}$

共通因数をまとめていきます。

$=(k+2)g_k(x)-xf_k(x)-x(k+1)f_k(x)$
$=(k+2)g_k(x)-xf_k(x)(1+k+1)$
$=(k+2)g_k(x)-(k+2)xf_k(x)$
$=(k+2)\{g_k(x)-xf_k(x)\}$

もう一度，$g_{n+1}(x)=g_n(x)-xf_n(x)$ を利用します。

$=(k+2)g_{k+1}(x)$

よって，$n=k+1$ のとき，（＊）は成り立つ。

[I]，[II]より，すべての正の整数 $n$ において

$\{f_{n+1}(x)\}’=(n+1)g_n(x)$，$\{g_{n+1}(x)\}’=-(n+1)f_n(x)$

が成り立つ。（証明終わり）

右辺から左辺を証明する

ここもやはり数学的帰納法を用いて証明していきますが，左辺から右辺を証明しようとするとうまくいきません。

そこで，等式の証明では右辺から左辺を証明するという方法もあったことを思い出しましょう。

$\sin n\theta=f_n(\tan\theta)\cos^n\theta$，$\cos n\theta=g_n(\tan\theta)\cos^n\theta$ ・・・（＊）

として

[I] $n=1$ のとき

$f_1(\tan\theta)\cos\theta$
$=\tan\theta\cos\theta$
$=\cfrac{\sin\theta}{\cos\theta}\cdot\cos\theta$
$=\sin\theta$

$g_1(\tan\theta)\cos\theta$
$=1\cdot\cos\theta$
$=\cos\theta$

よって，$n=1$ のとき，（＊）は成り立つ。

[II] $n=k$ のとき（＊）が成り立つと仮定して，$n=k+1$ とすると

$f_{k+1}(\tan\theta)\cos^{k+1}\theta$

問題文の条件，$f_{n+1}(x)=f_n(x)+xg_n(x)$ を用います。

$=\{f_k(\tan\theta)+\tan\theta g_k(\tan\theta)\}\cos^{k+1}\theta$
$=f_k(\tan\theta)\cos^{k+1}\theta+\tan\theta\cos^{k+1}\theta g_k(\tan\theta)$

ここで，$\tan\theta\cos^{k+1}\theta$ は

$=\cfrac{\sin\theta}{\cos\theta}\cdot\cos^k\theta\cdot\cos\theta$
$=\sin\theta\cos^k\theta$

となるので

$=f_k(\tan\theta)\cos^{k+1}\theta +\sin\theta\cos^k\theta g_k(\tan\theta)$
$=f_k(\tan\theta)\cos^k\theta\cos\theta +\sin\theta\cos^k\theta g_k(\tan\theta)$

仮定である $\sin n\theta=f_n(\tan\theta)\cos^n\theta$，$\cos n\theta=g_n(\tan\theta)\cos^n\theta$ を代入します。

$=\sin k\theta\cdot\cos\theta+\sin\theta\cdot\cos k\theta$
$=\sin k\theta\cdot\cos\theta+\cos k\theta\cdot\sin\theta$

この式は加法定理になっています。

$=\sin(k\theta+\theta)$
$=\sin(k+1)\theta$

これで証明ができました。同様にして

$g_{k+1}(\tan\theta)\cos^{k+1}\theta$
$=\{g_k(\tan\theta)-\tan\theta f_k(\tan\theta)\}\cos^{k+1}\theta$
$=g_k(\tan\theta)\cos^{k+1}\theta-\sin\theta f_k(\tan\theta)\cos^k\theta$
$=\cos k\theta\cos\theta-\sin k\theta\sin\theta$
$=\cos(k\theta+\theta)$
$=\cos(k+1)\theta$

[I]，[II]より，すべての正の整数 $n$ において

$\sin n\theta=f_n(\tan\theta)\cos^n\theta$，$\cos n\theta=g_n(\tan\theta)\cos^n\theta$ $\Big(-\cfrac{\pi}{2}<\theta<\cfrac{\pi}{2}\Big)$

が成り立つ。（証明終わり）

tan ですべての実数を表せることを利用する

方程式の解を求めるということは，$x$ の値を求めるということです。とはいえ，$x$ のままでは方程式はまったく解けません。

そこで，(2)の式を利用することを考えます。

$\tan\theta$ は $-\cfrac{\pi}{2}<\theta<\cfrac{\pi}{2}$ の区間においてすべての実数をとります。つまり，$x$ の代わりに $\tan\theta$ の値を求めることで方程式を解くこともできるのです。

$f_n(x)=ag_n(x)$

$x=\tan\theta$ として

$f_n(\tan\theta)=ag_n(\tan\theta)$

(2)より

$\sin n\theta=f_n(\tan\theta)\cos^n\theta$
$f_n(\tan\theta)=\cfrac{\sin n\theta}{\cos^n\theta}$

また

$\cos n\theta=g_n(\tan\theta)\cos^n\theta$
$g_n(\tan\theta)=\cfrac{\cos n\theta}{\cos^n\theta}$

となるので

$f_n(\tan\theta)=ag_n(\tan\theta)$
$\cfrac{\sin n\theta}{\cos^n\theta}=a\cdot\cfrac{\cos n\theta}{\cos^n\theta}$
$\sin n\theta=a\cos n\theta$
$a=\cfrac{\sin n\theta}{\cos n\theta}$
$=\tan n\theta$

また

$-\cfrac{\pi}{2}<\theta<\cfrac{\pi}{2}$
$-\cfrac{n\pi}{2}<n\theta<\cfrac{n\pi}{2}$

となります。

数IIの微分で定数分離という考え方を習っていると思います。それと同じ要領で $\tan n\theta=a$ の解の個数を考えていきます。

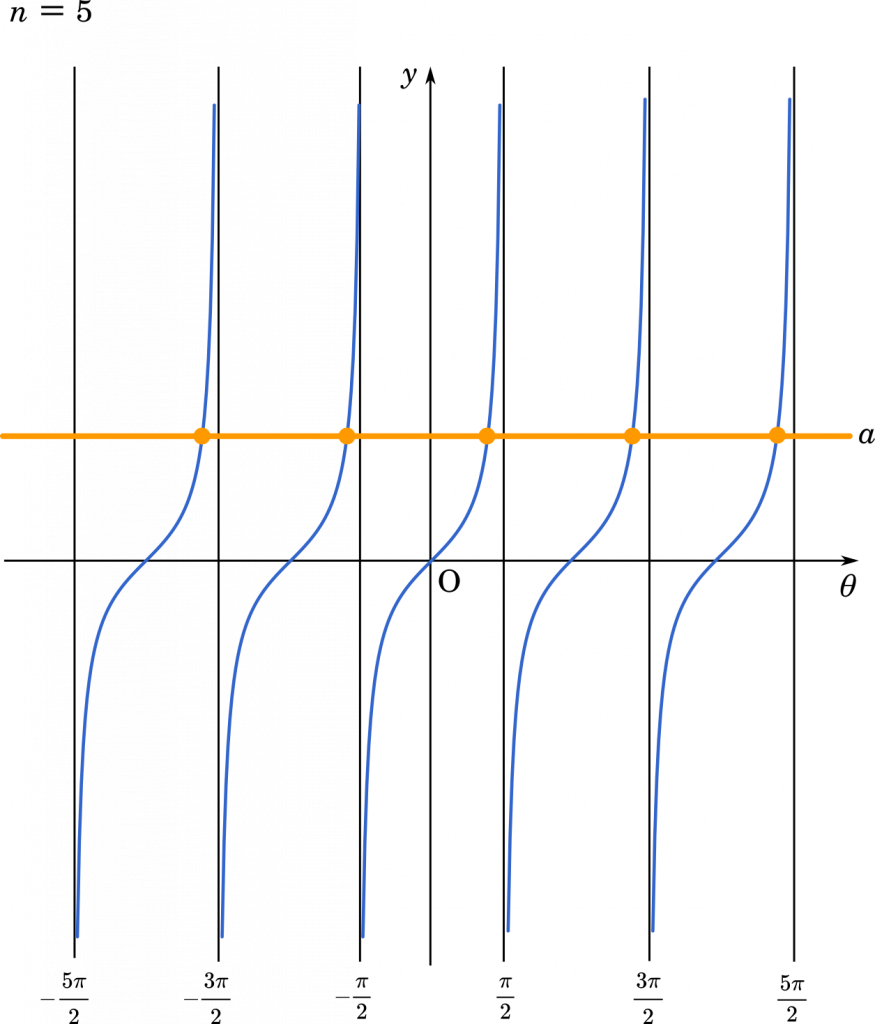
例えば $n=5$ のときは上のようなグラフになります。

こうしてグラフにしてみると分かりますが，結局 $a$ の値に関係なく $n=5$ のとき解の個数は 5 個になります。

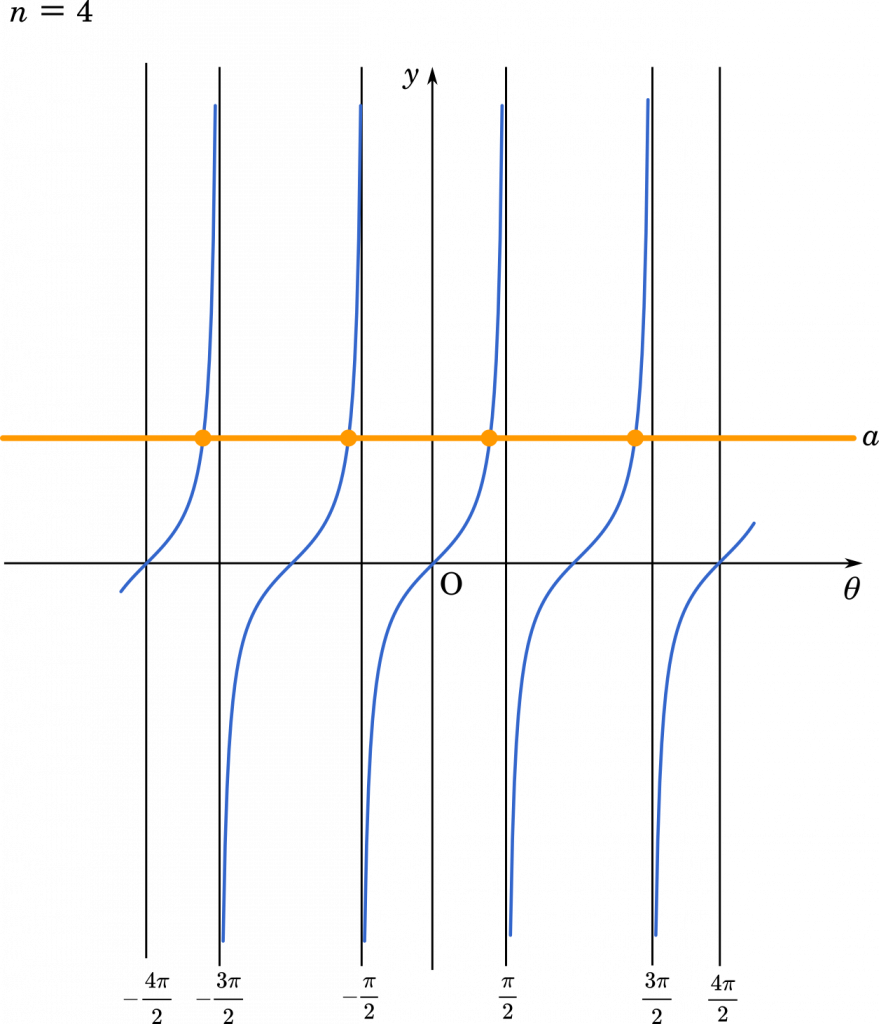
$n=4$ なら上のようなグラフになります。このように，$n$ が偶数でも奇数でも解の個数は $n$ 個になることが分かります。

ただし，これには 1 つだけ例外があります。

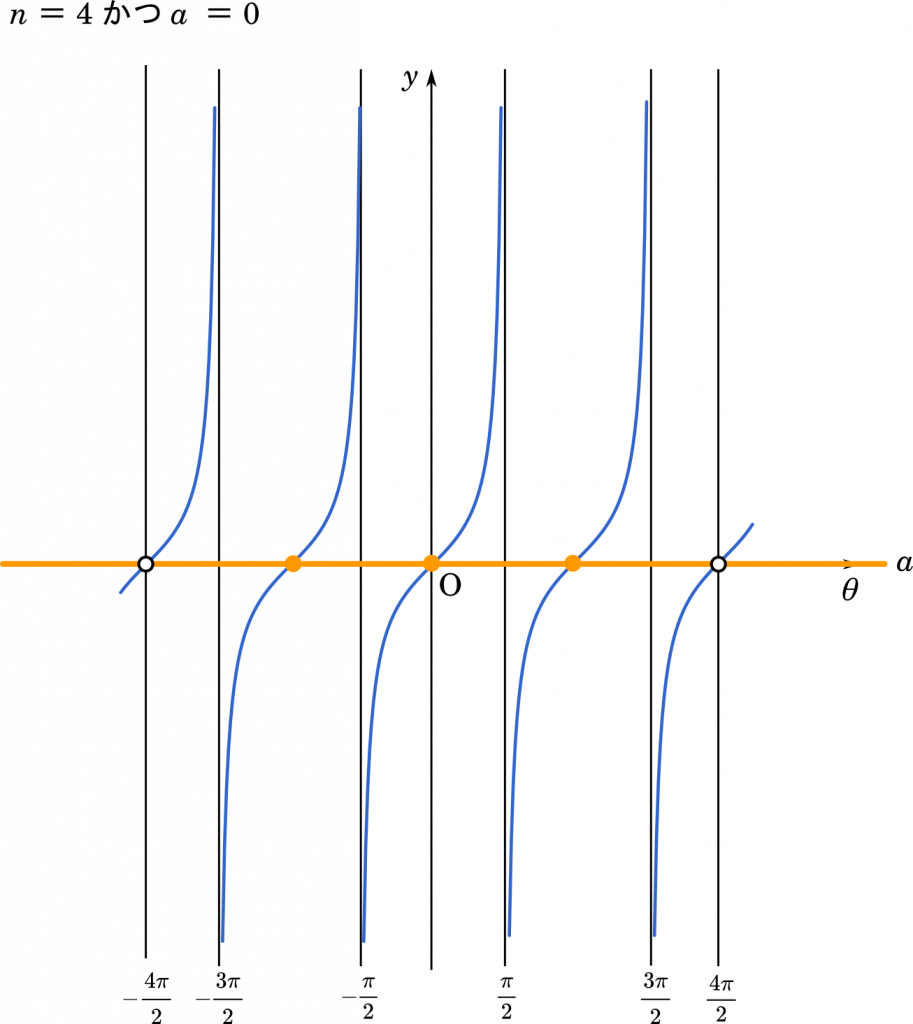
$n$ が偶数かつ $a=0$ だと，範囲の両端の部分が解に含まれないことになります。

したがって，解の個数は

$a=0$ かつ $n$ が偶数のとき $n-1$ 個
それ以外は $n$ 個（答え）