【数IIB相加・相乗平均】2 辺のなす角の最大を求める（神戸大2021第3問）

三角形の面積を利用する

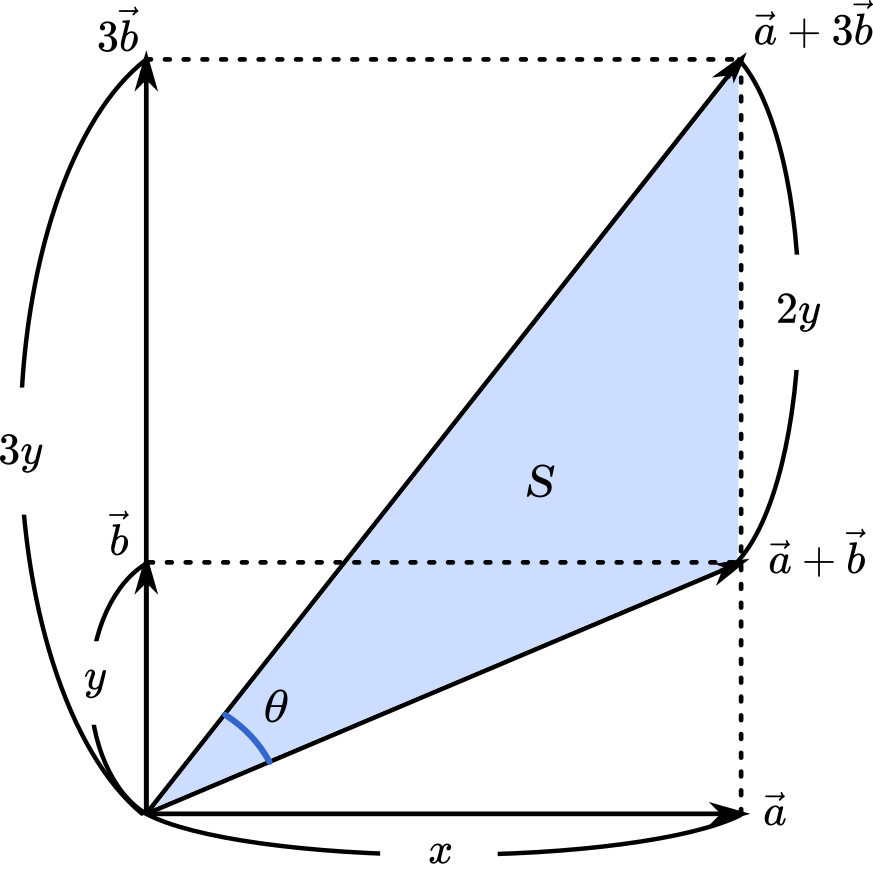
上でつくった三角形の面積を利用して解きます。

三角形は底辺 $2y$，高さ $x$ だから，面積は

$S=\cfrac{1}{2}\cdot2y\cdot x$
$=xy$ ・・・①

また，三角比を用いて面積を出すこともできます。

斜辺の長さは三平方の定理を用います。

$S=\cfrac{1}{2}\sqrt{x^2+y^2}\sqrt{x^2+9y^2}\sin\theta$
$S^2=\cfrac{1}{4}(x^2+y^2)(x^2+9y^2)\sin^2\theta$

①，②より

$x^2y^2=\cfrac{1}{4}(x^2+y^2)(x^2+9y^2)\sin^2\theta$

$\sin^2\theta=\cfrac{4x^2y^2}{(x^2+y^2)(x^2+9y^2)}$　（答え）

相加・相乗平均

(2) $\theta$ の最大値を求めよ。

相加・相乗平均を用いて $\sin^2\theta$ の最大値を求めます。

$\sin^2\theta=\cfrac{4x^2y^2}{(x^2+y^2)(x^2+9y^2)}$
$=\cfrac{4x^2y^2}{x^4+9x^2y^2+x^2y^2+9y^4}$
$=\cfrac{4x^2y^2}{x^4+10x^2y^2+9y^4}$

分母と分子の両方に文字があると最大や最小を考えることができません。こういう場合は，分母・分子どちらかの文字を消去することを考えます。

分母・分子を $x^2y^2$ で割ると

$=\cfrac{4}{\cfrac{x^2}{y^2}+10+\cfrac{9y^2}{x^2}}$
$=\cfrac{4}{\cfrac{x^2}{y^2}+\cfrac{9y^2}{x^2}+10}$

ここから，$\cfrac{x^2}{y^2}$ と $\cfrac{9y^2}{x^2}$ をかけると文字が消えることを利用して，相加・相乗平均に持ち込みます。

相加・相乗平均より

$\cfrac{x^2}{y^2}+\cfrac{9y^2}{x^2}\geqq2\sqrt{\cfrac{x^2}{y^2}\cdot\cfrac{9y^2}{x^2}}$
$\geqq2\sqrt{9}$
$\geqq6$

したがって，$\sin^2\theta$ の最大値は

$\sin^2\theta=\cfrac{4}{6+10}=\cfrac{1}{4}$
$\sin\theta=\pm\cfrac{1}{2}$

$0\leqq\theta\leqq\pi$ より

$\sin\theta=\cfrac{1}{2}$

これに当てはまる $\theta$ は第1象限と第2象限の 2 つがあります。しかし，最初の図を見れば想像できるように $\theta$ が $\cfrac{\pi}{2}$ を超えることはなさそうです。

しかし，解答としては $\theta$ が $\cfrac{\pi}{2}$ を超えないということを数式で示すべきです。

余弦定理より

$(2y)^2=(\sqrt{x^2+y^2})^2+(\sqrt{x^2+9y^2})^2-2\sqrt{x^2+y^2}\sqrt{x^2+9y^2}\cos\theta$
$\cos\theta=\cfrac{2x^2+6y^2}{2\sqrt{x^2+y^2}\sqrt{x^2+9y^2}}$
$\cos\theta=\cfrac{x^2+3y^2}{\sqrt{x^2+y^2}\sqrt{x^2+9y^2}}$

$x\geqq0$，$y\geqq0$ より

$\cos\theta\geqq0$

よって，$0\leqq\theta\leqq\cfrac{\pi}{2}$ だから

$\theta=\cfrac{\pi}{6}$　（答え）