【数IA三角比】塔の高さを三角比で求める問題／三角比で高さ・底辺を求める考え方(神戸大文系第3問)

水平な地面に一本の塔が垂直に建っている（太さは無視する）。塔の先端を P とし，足元の地点を H とする。また，H を通らない一本の道が一直線に伸びている（幅は無視する）。道の途中に 3 地点 A，B，C がこの順にあり，BC ＝ 2AB をみたしている。以下の問に答えよ。

(1) $2\text{AH}^2-3\text{BH}^2+\text{CH}^2=6\text{AB}^2$ が成り立つことを示せ。

(2) A，B，C から P を見上げた角度 $\angle\text{PAH}$，$\angle\text{PBH}$，$\angle\text{PCH}$ はそれぞれ 45°，60°，30° であった。AB ＝ 100m のとき，党の高さ PH (m) の整数部分を求めよ。

(3) (2)において，H と道の距離 (m) の整数部分を求めよ。

余弦定理

(1) $2\text{AH}^2-3\text{BH}^2+\text{CH}^2=6\text{AB}^2$ が成り立つことを示せ。

ここは余弦定理を使っていきます。

余弦定理 $a^2=b^2+c^2-2bc\cos A$

余弦定理やってみたけど，式が複雑になってうまくいかなかったです。

どんな感じで計算したの？

こんな感じで，角を $\alpha,\beta$ でおきました。

それは角の作り方がマズい。

角は上のように置いて，１か所で対処すべきです。△ABH と △ACH について考え，それらに共通する角を $\theta$ とします。

△ABH と △ACH について余弦定理を用います。

$\text{BH}^2=\text{AH}^2+\text{AB}^2-2\text{AH}\cdot\text{AB}\cos\theta$ ・・・①

$\text{AC}=3\text{AB}$ より

$\text{CH}^2=\text{AH}^2+(3\text{AB})^2-2\text{AH}\cdot3\text{AB}\cos\theta$ ・・・②

①×3 － ②

$3\text{BH}^2-\text{CH}^2=2\text{AH}^2-6\text{AB}^2$

$2\text{AH}^2-3\text{BH}^2+\text{CH}^2=6\text{AB}^2$　（証明終わり）

塔の高さ

△AHP は $1:1:\sqrt{2}$ の三角形です。そこから

$\text{PH}=\text{AH}$ ・・・③

が成り立ちます。

次に，△BHP は $1:2:\sqrt{3}$ の三角形です。

$\text{BH}:\text{PH}=1:\sqrt{3}$
$\text{PH}=\sqrt{3}\text{BH}$
$\text{BH}=\cfrac{\text{PH}}{\sqrt{3}}$ ・・・④

さらに，△CHP も $1:2:\sqrt{3}$ の三角形です。

$\text{CH}:\text{PH}=\sqrt{3}:1$
$\text{CH}=\sqrt{3}\text{PH}$ ・・・⑤

これらを(1)の式に代入すると

$2\text{AH}^2-3\text{BH}^2+\text{CH}^2=6\text{AB}^2$
$2\text{PH}^2-3\Big(\cfrac{\text{PH}}{\sqrt{3}}\Big)^2+(\sqrt{3}\text{PH})^2=6\text{AB}^2$
$2\text{PH}^2-\text{PH}^2+3\text{PH}^2=6\text{AB}^2$
$4\text{PH}^2=6\text{AB}^2$

$\text{PH}\geqq0$，$\text{AB}\geqq0$ より

$2\text{PH}=\sqrt{6}\text{AB}$
$\text{PH}=\cfrac{\sqrt{6}}{2}\text{AB}$

$\text{AB}=100$ より

$\text{PH}=50\sqrt{6}$

答えは整数で求めます。そこで，$50\sqrt{6}$ はいくつになるかを考えなければなりません。

$\sqrt{2}$ が 1.41 くらいなのは覚えてるけど,$\sqrt{6}$ は覚えてないです。

平方根のおおよその値は計算できるようになって。

$\sqrt{4}<\sqrt{6}<\sqrt{9}$ より

$2<\sqrt{6}<3$

$\sqrt{6}$ は 2 と 3 の間のどこかです。ここからは値をあてはめながら範囲を絞り込んでいきます。

たとえば，真ん中をとって 2.5 の 2 乗を考えてみます。

$2.5^2=6.25$

6 を超えました。そこで，2.4 の 2 乗を試します。

$2.4^2=5.76$

6 を下回りました。

ここから，$2.4<\sqrt{6}<2.5$ が分かります。さらに絞り込んでいきましょう。

$2.45^2=6.0025$
$2.44^2=5.9536$

よって $2.44<\sqrt{6}<2.45$

ここから

$50\times2.44=122$
$50\times2.45=122.5$

ここまで絞り込めば整数部分は 122 ということで間違いありません。

したがって，122m　（答え）

距離を求める

距離ってどこの長さ？

点と直線の間に線を引いたときに，その線がもっとも短くなるヤツを距離という。

点 H から直線に下ろした垂線の足を D とすると，AD⊥DH となります。このとき，DH が距離です。

DH は三角比を使って

$\text{DH}=\text{AH}\sin\theta$

で求められます。

三角比で底辺と高さを求める

なんでこれで長さ出せるのか分からないです。

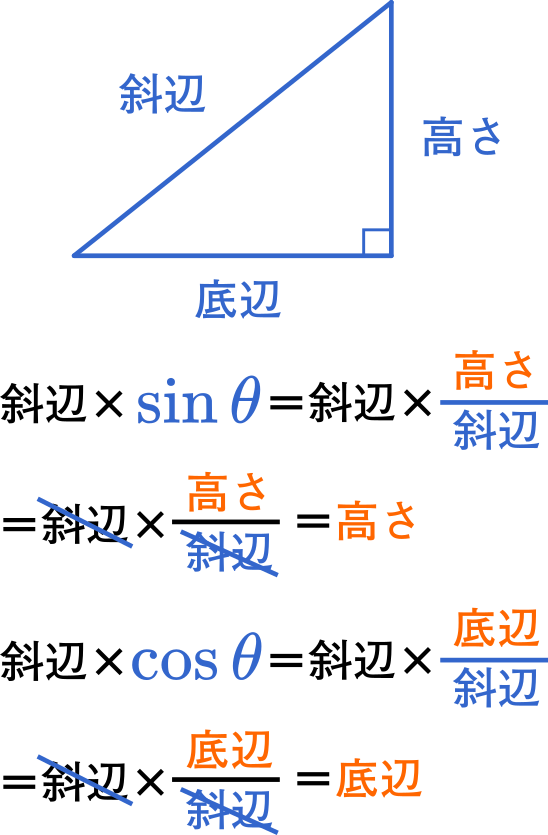
考え方は上のようになります。

三角比のもともとの定義を思い出しましょう。

直角三角形があるとき，$\cfrac{\textsf{高さ}}{\textsf{斜辺}}$ の値が $\sin$ で，$\cfrac{\textsf{底辺}}{\textsf{斜辺}}$ の値が $\cos$ でした。

$\textsf{斜辺}\times\sin\theta=\textsf{斜辺}\times\cfrac{\textsf{高さ}}{\textsf{斜辺}}$

となるので，約分すると

$=\cancel{\textsf{斜辺}}\times\cfrac{\textsf{高さ}}{\cancel{\textsf{斜辺}}}=\textsf{高さ}$

こうして高さが求められます。

同じようにして，斜辺に $\cos$ をかければ底辺が分かります。

sin を求めて距離を出す

問題に戻りましょう。

こうなると，$\sin\theta$ の値が必要です。

(2)より BH の長さは分かるので，△ABH を使ってみます。

$\text{BH}=\cfrac{\text{PH}}{\sqrt{3}}$ より

$\text{AH}=\text{PH}$ だから

$\text{BH}=\cfrac{\text{AH}}{\sqrt{3}}$
$=\cfrac{50\sqrt{6}}{\sqrt{3}}$
$=50\sqrt{2}$

また，$\text{AB}=100$ だから

$\text{AH}:\text{AB}:\text{BH}=50\sqrt{6}:100:50\sqrt{2}$
$=\sqrt{6}:2:\sqrt{2}$

ここから余弦定理を用いていったん $\cos$ の値を求めます。このとき，辺の長さをそのまま用いても計算できますが，代わりに辺の比を使うこともできます。

三角形がたがいに相似の関係なら角度同じだからね。

余弦定理より

$(\sqrt{2})^2=(\sqrt{6})^2+2^2-2\cdot\sqrt{6}\cdot2\cos\theta$
$2=6+4-4\sqrt{6}\cos\theta$
$4\sqrt{6}\cos\theta=8$
$\cos\theta=\cfrac{2}{\sqrt{6}}$

ここから $\sin\theta$ を求めます。

$\sin^2\theta+\Big(\cfrac{2}{\sqrt{6}}\Big)^2=1$
$\sin^2\theta=1-\cfrac{2}{3}=\cfrac{1}{3}$
$\sin\theta=\cfrac{1}{\sqrt{3}}$

ようやく $\sin\theta$ の値が求められました。

$\text{DH}=\text{AH}\sin\theta$ だから

$\text{DH}=122\cdot\cfrac{1}{\sqrt{3}}$

$\sqrt{3}$ の値は覚えてる？

これは分かります。1.73 です。

$=\cfrac{122}{1.73}=70.5\cdots$

したがって整数部分は 70m。（答え）