内接円の中心が描く軌跡/媒介変数と回転体の体積(神戸大2020理系第2問)
$\theta$ を $0<\theta<\cfrac{\pi}{2}$ をみたす実数とし,原点 O,A$(1,0)$,B$(\cos2\theta,\sin2\theta)$ を頂点とする△OABの内接円の中心を P とする。また,$\theta$ がこの範囲を動くときに点 P が描く曲線と線分 OA によって囲まれた部分を $D$ とする。以下の問に答えよ。
(1) 点 P の座標は $\Big(1-\sin\theta,\cfrac{\sin\theta\cos\theta}{1+\sin\theta}\Big)$ で表されることを示せ。
(2) $D$ を $x$ 軸のまわりに 1 回転させてできる立体の体積を求めよ。
内接円の中心の座標
(1) 点 P の座標は $\Big(1-\sin\theta,\cfrac{\sin\theta\cos\theta}{1+\sin\theta}\Big)$ で表されることを示せ。
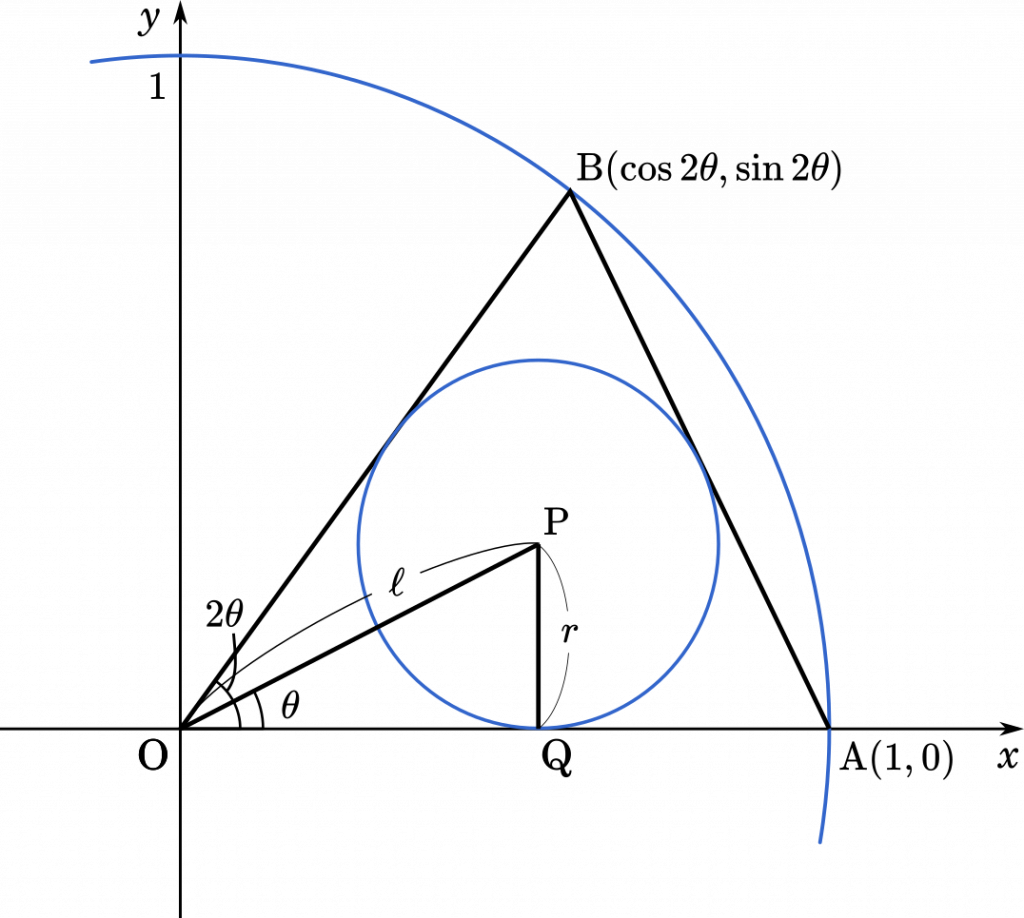
このように図を描いてみると,△OPQ のそれぞれの辺の長さがわかれば,点 P の座標が求められそうです。

公式 $S=\cfrac{1}{2}r(a+b+c)$
これを使って $r$ を求めたいのですが,そのためには $r$ 以外の値がわかっていなければなりません。
まず △OAB は底辺が 1,高さが $\sin2\theta$ なので,面積は
$S=\cfrac{1}{2}\cdot1\cdot\sin2\theta$
$=\cfrac{1}{2}\sin2\theta$
となります。
また,△OAB は OA = OB の二等辺三角形で辺の長さは 1 です。あとは AB の長さが必要なので,余弦定理で求めましょう。
余弦定理 $a^2=b^2+c^2-2bc\cos\theta$
$\text{AB}^2=1^2+1^2-2\cdot1\cdot1\cdot\cos2\theta$
$=2-2\cos2\theta$
$=2(1-\cos2\theta)$
半角の公式 $\sin^2\theta=\cfrac{1-\cos2\theta}{2}$
$=4\cdot\cfrac{1-\cos2\theta}{2}$
$=4\sin^2\theta$
$\text{AB}=2\sin\theta$
最初の公式にもどりましょう。
$S=\cfrac{1}{2}r(a+b+c)$ より
$\cfrac{1}{2}\sin2\theta=\cfrac{1}{2}r(1+1+2\sin\theta)$
$r=\cfrac{\sin2\theta}{2+2\sin\theta}$
2 倍角の公式 $\sin2\theta=2\sin\theta\cos\theta$
$=\cfrac{2\sin\theta\cos\theta}{2+2\sin\theta}$
$=\cfrac{\sin\theta\cos\theta}{1+\sin\theta}$
このとき $r$ が点 P の $y$ 座標ということになります。
あとは三角比を使って OQ の長さを求めます。
$\cfrac{r}{\text{OQ}}=\tan\theta$ より
$\cfrac{r}{\text{OQ}}=\cfrac{\sin\theta}{\cos\theta}$
$\text{OQ}=\cfrac{\cos\theta}{\sin\theta}\cdot r$
$=\cfrac{\cos\theta}{\sin\theta}\cdot\cfrac{\sin\theta\cos\theta}{1+\sin\theta}$
$=\cfrac{\cos^2\theta}{1+\sin\theta}$
$=\cfrac{1-\sin^2\theta}{1+\sin\theta}$
$=\cfrac{(1+\sin\theta)(1-\sin\theta)}{1+\sin\theta}$
$=1-\sin\theta$
したがって
点 P の座標は $\Big(1-\sin\theta,\cfrac{\sin\theta\cos\theta}{1+\sin\theta}\Big)$
(答え)
回転体の体積
(2) $D$ を $x$ 軸のまわりに 1 回転させてできる立体の体積を求めよ。


点 P の座標は(1)で $\Big(1-\sin\theta,\cfrac{\sin\theta\cos\theta}{1+\sin\theta}\Big)$ となっていますが,このままでは $\theta$ の値が変化するときに,点 P がどのような曲線をつくるのかがイマイチわかりません。
そこで,いったん増減表をつくって点 P が描く曲線の概形を考えてみましょう。
$x=1-\sin\theta$
$y=\cfrac{\sin\theta\cos\theta}{1+\sin\theta}$
として
$\cfrac{dx}{d\theta}=-\cos\theta$
商の微分 $\Big\{\cfrac{f(x)}{g(x)}\Big\}’=\cfrac{f'(x)g(x)-f(x)g'(x)}{\{g(x)\}^2}$
$\cfrac{dy}{d\theta}=\cfrac{(\sin\theta\cos\theta)'(1+\cos\theta)-\sin\theta\cos\theta(1+\sin\theta)’}{(1+\sin\theta)^2}$
$(\sin\theta\cos\theta)’$ の部分は積の微分を使います。
積の微分 $\{f(x)g(x)\}’=f'(x)g(x)+f(x)g'(x)$
$=\cfrac{(\cos^2\theta-\sin^2\theta)(1+\sin\theta)-\sin\theta\cos^2\theta}{(1+\sin\theta)^2}$
式を $\sin$ に合わせていきます。
$=\cfrac{(1-\sin^2\theta-\sin^2\theta)(1+\sin\theta)-\sin\theta(1-\sin^2\theta)}{(1+\sin\theta)^2}$
$=\cfrac{(1-2\sin^2\theta)(1+\sin\theta)-\sin\theta+\sin^3\theta}{(1+\sin\theta)^2}$
$=\cfrac{1+\sin\theta-2\sin^2\theta-2\sin^3\theta-\sin\theta+\sin^3\theta}{(1+\sin\theta)^2}$
$=\cfrac{-\sin^3\theta-2\sin^2\theta+1}{(1+\sin\theta)^2}$
ここで,いったん $\sin\theta=k$ とすると
$=-\cfrac{k^3+2k^2-1}{(1+k)^2}$
因数分解します。
$k=-1$ のとき,$k^3+2k^2-1=0$ となるので,$k^3+2k^2-1$ は $k+1$ で因数分解できます。
組立除法を用いて
$\begin{matrix}1&2&0&-1&|\underline{-1}\\&-1&-1&1\\\hline 1&1&-1&0\end{matrix}$
$=-\cfrac{(k+1)(k^2+k-1)}{(1+k)^2}$
$=-\cfrac{k^2+k-1}{1+k}$
$=-\cfrac{\sin^2\theta+\sin\theta-1}{1+\sin\theta}$
極値を求めます。
$\cfrac{dx}{d\theta}$ について
$-\cos\theta=0$ とすると
$\theta=\cfrac{\pi}{2}$
$\cfrac{dy}{d\theta}$ について
$-\cfrac{\sin^2\theta+\sin\theta-1}{1+\sin\theta}=0$ とすると
$\sin^2\theta+\sin\theta-1=0$
$0<\theta<\cfrac{\pi}{2}$ より
$\sin\theta=\cfrac{-1+\sqrt{5}}{2}$
増減表は
$\def\arraystretch{1.5}\begin{array}{|c||c|c|c|c|c|}\hline\theta&(0)&\cdots&\alpha&\cdots&(\frac{\pi}{2})\\\hline\frac{dx}{d\theta}&(-1)&-&&-&(0)\\\hline x&(1)&\searrow&&\searrow&(0)\\\hline \frac{dy}{d\theta}&(1)&+&0&-&(-\frac{1}{2})\\\hline y&(0)&\nearrow&\frac{-1+\sqrt{5}}{2}&\searrow&(0)\\\hline\end{array}$

点 P の描く曲線はオレンジの部分になります。
回転体の体積を求めましょう。
$\displaystyle S=\int_0^1\pi y^2dx$
ただし,$y=\cfrac{\sin\theta\cos\theta}{1+\sin\theta}$ なので,$\theta$ の式を $x$ で積分することはできません。そこで $dx$ を $d\theta$ に置換しましょう。
$x=1-\sin\theta$ より
$dx=-\cos\theta\space d\theta$
$\def\arraystretch{1.5}\begin{array}{c|c}x&0\rightarrow1\\\hline\theta&\frac{\pi}{2}\rightarrow0\end{array}$
$\displaystyle=\pi\int_{\small{\frac{\pi}{2}}}^0\cfrac{\sin^2\theta\cos^2\theta}{(1+\sin\theta)^2}\cdot(-\cos\theta)d\theta$
$\displaystyle=-\pi\int_{\small{\frac{\pi}{2}}}^0\cfrac{\sin^2\theta\cos^3\theta}{(1+\sin\theta)^2}\space d\theta$
積分区間をひっくり返しておきましょう。
$\displaystyle=\pi\int_0^{\small{\frac{\pi}{2}}}\cfrac{\sin^2\theta\cos^3\theta}{(1+\sin\theta)^2}\space d\theta$
このまま積分していっても良いのですが,おそらく計算式が複雑なことになります。そこでもう一度置換して計算しやすくしておきましょう。
$\sin\theta=t$ とすると
$\cos\theta\space d\theta=dt$
$\def\arraystretch{1.5}\begin{array}{c|c}\theta&0\rightarrow\frac{\pi}{2}\\\hline t&0\rightarrow1\end{array}$
$\cos^3\theta$ の部分は
$\cos^3\theta=\cos^2\theta\cdot\cos\theta$
$=(1-\sin^2\theta)\cos\theta$
と変形できるので
$=\displaystyle\pi\int_0^1\cfrac{t^2(1-t^2)}{(1+t)^2}\space dt$
$=\displaystyle\pi\int_0^1\cfrac{t^2(1+t)(1-t)}{(1+t)^2}\space dt$
$=\displaystyle\pi\int_0^1\cfrac{t^2(1-t)}{1+t}\space dt$
$=\displaystyle\pi\int_0^1\cfrac{t^2-t^3}{1+t}\space dt$


ここで
$\cfrac{t^2-t^3}{1+t}$
$=\cfrac{t^2}{1+t}-\cfrac{t^3}{1+t}$
$=\cfrac{t^2-1+1}{1+t}-\cfrac{t^3+1-1}{1+t}$
$=\cfrac{(t+1)(t-1)+1}{1+t}-\cfrac{(t+1)(t^2-t+1)-1}{1+t}$
$=t-1+\cfrac{1}{1+t}-t^2+t-1+\cfrac{1}{1+t}$
$=-t^2+2t-2+\cfrac{2}{1+t}$
となるので
$\displaystyle S=\pi\int_0^1-t^2+2t-2+\cfrac{2}{1+t}\space dt$
$=\pi\Big[-\cfrac{t^3}{3}+t^2-2t+2\log(1+t)\Big]_0^1$
$=\pi\Big(-\cfrac{1}{3}+1-2+2\log 2\Big)$
$=\pi\Big(2\log2-\cfrac{4}{3}\Big)$ (答え)
SNSでシェア