正四面体の中につくる三角柱の体積と数列の極限(神戸大2017理系第3問)

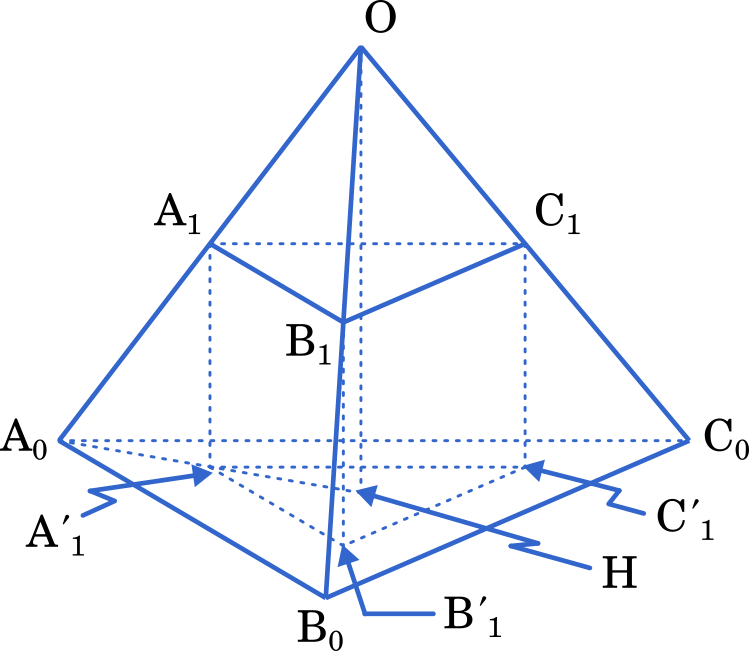
1 辺の長さが $a_0$ の正四面体 $\text{OA}_0\text{B}_0\text{C}_0$ がある。図のように，辺 $\text{OA}_0$ 上の点 $\text{A}_1$，辺 $\text{OB}_0$ 上の点 $\text{B}_1$，辺 $\text{OC}_0$ 上の点 $\text{C}_1$ から平面 $\text{A}_0\text{B}_0\text{C}_0$ に降ろされた垂線をそれぞれ $\text{A}_1\text{A}’_1,\text{B}_1\text{B}’_1,\text{C}_1\text{C}’_1$ としたとき，三角柱 $\text{A}_1\text{B}_1\text{C}_1-\text{A}’_1\text{B}’_1\text{C}’_1$ は正三角柱になるとする。ただし，ここでは底面が正三角形であり，側面が正方形である三角柱を正三角柱とよぶことにする。同様に，点 $\text{A}_2,\text{B}_2,\text{C}_2,\text{A}’_2,\text{B}’_2,\text{C}’_2,\cdots\cdots$ を次にように定める。正四面体 $\text{OA}_k\text{B}_k\text{C}_k$ において，辺 $\text{OA}_k$ 上の点 $\text{A}_{k+1}$，辺 $\text{OB}_k$ 上の点 $\text{B}_{k+1}$，辺 $\text{OC}_k$ 上の点 $\text{C}_{k+1}$ から平面 $\text{A}_k\text{B}_k\text{C}_k$ に下ろした垂線をそれぞれ $\text{A}_{k+1}\text{A}’_{k+1},\text{B}_{k+1}\text{B}’_{k+1},\text{C}_{k+1}\text{C}’_{k+1}$ としたとき，三角柱 $\text{A}_{k+1}\text{B}_{k+1}\text{C}_{k+1}-\text{A}’_{k+1}\text{B}’_{k+1}\text{C}’_{k+1}$ は正三角柱になるとする。辺 $\text{A}_k\text{B}_k$ の長さを $a_k$ とし，正三角柱 $\text{A}_k\text{B}_k\text{C}_k-\text{A}’_k\text{B}’_k\text{C}’_k$ の体積を $V_k$ とするとき，以下の問に答えよ。

(1) 点 O から平面 $\text{A}_0\text{B}_0\text{C}_0$ に下ろした垂線を OH とし，$\theta=\angle\text{OA}_0\text{H}$ とするとき，$\cos\theta$ と $\sin\theta$ の値を求めよ。

(2) $a_1$ を $a_0$ を用いて表せ。

(3) $V_k$ を $a_0$ を用いて表し，$\displaystyle\sum_{k=1}^\infty V_k$ を求めよ。

四面体の扱い方

(1)から始めます。

入試問題において正四面体はよく扱われる題材です。ここでは最も基本的な方法に立ち返って考えていきます。

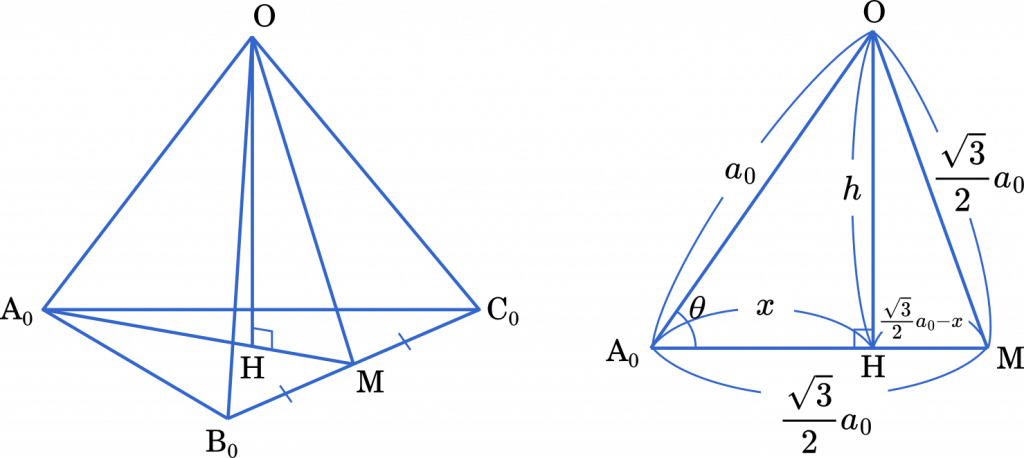
まず，辺 $\text{B}_0\text{C}_0$ の中点を M とします。

$\triangle\text{O}\text{B}_0\text{C}_0$ は正三角形なので，$\angle\text{O}\text{B}_0\text{M}=60\degree$ です。よって，$\triangle\text{O}\text{B}_0\text{M}$ は辺の比が $1:2:\sqrt{3}$ の直角三角形になります。$\text{O}\text{B}_0=a_0$ から，$\text{OM}=\cfrac{\sqrt{3}}{2}a_0$ となります。AM も同様に $\cfrac{\sqrt{3}}{2}a_0$ です。

次に，$\triangle\text{O}\text{A}_0\text{M}$ について考えてみましょう。上の図のように $x$ と $h$ を定めます。

三平方の定理より

${a_0}^2-x^2=h^2$
$\Big(\cfrac{\sqrt{3}}{2}a_0\Big)^2-\Big(\cfrac{\sqrt{3}}{2}a_0-x\Big)^2=h$

よって

${a_0}^2-x^2=\Big(\cfrac{\sqrt{3}}{2}a_0\Big)^2-\Big(\cfrac{\sqrt{3}}{2}a_0-x\Big)^2$
$=\cfrac{3}{4}{a_0}^2-\cfrac{3}{4}{a_0}^2+\sqrt{3}a_0x-x^2$
$=\sqrt{3}a_0x-x^2$
${a_0}^2=\sqrt{3}a_0x$
$x=\cfrac{{a_0}^2}{\sqrt{3}a_0}=\cfrac{a_0}{\sqrt{3}}$

三平方の定理より

$h^2={a_0}^2-x^2$
$={a_0}^2-\cfrac{{a_0}^2}{3}=\cfrac{2}{3}{a_0}^2$
$h=\cfrac{\sqrt{6}}{3}a_0$

したがって

$\cos\theta=\cfrac{x}{a_0}=\cfrac{\sqrt{3}}{3}$

$\sin\theta=\cfrac{h}{a_0}=\cfrac{\sqrt{6}}{3}$

（答え）

三角柱の高さを求める

(2)に進みます。

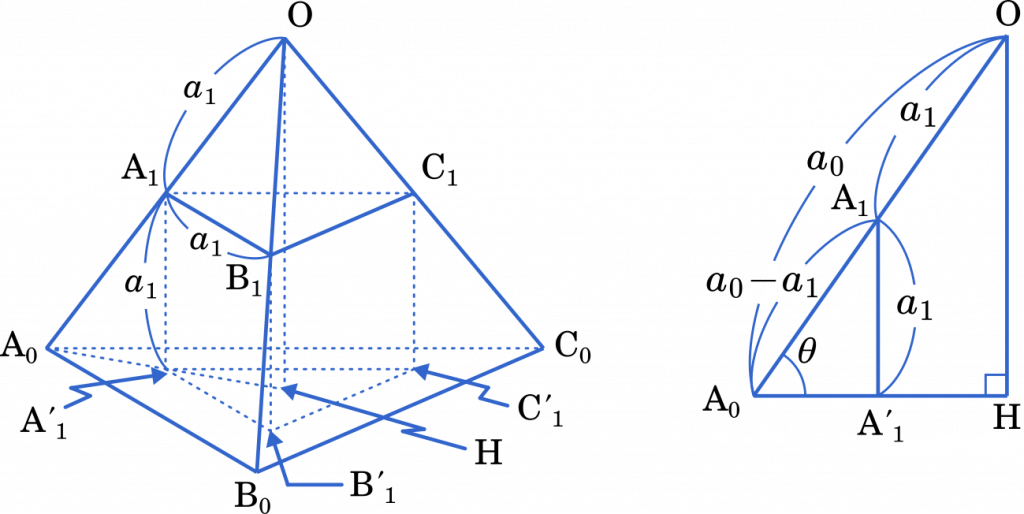
$\triangle\text{O}\text{A}_1\text{B}_1$ は正三角形なので，$\text{A}_1\text{B}_1=a_1$ です。また，正三角柱の側面は正方形なので，$\text{A}_1\text{A}’_1=a_1$ となります。

$(a_0-a_1)\sin\theta=a_1$
$(a_0-a_1)\cfrac{\sqrt{6}}{3}=a_1$
$a_0-a_1=\cfrac{3}{\sqrt{6}}a_1=\cfrac{\sqrt{6}}{2}a_1$
$\Big(1+\cfrac{\sqrt{6}}{2}\Big)a_1=a_0$
$a_1=\cfrac{a_0}{1+\cfrac{\sqrt{6}}{2}}$
$=\cfrac{2a_0}{2+\sqrt{6}}$
$=\cfrac{2a_0(2-\sqrt{6})}{(2+\sqrt{6})(2-\sqrt{6})}$
$=\cfrac{2a_0(2-\sqrt{6})}{-2}$
$=(\sqrt{6}-2)a_0$　（答え）

体積と極限

(3)に進みます。

正三角形の面積に高さをかければ正三角柱の体積が求められます。

正三角形の面積は，公式 $\cfrac{1}{2}ab\sin C$ を用いましょう。

$V_k=\cfrac{1}{2}a_k\cdot a_k\sin60\degree\cdot a_k$
$=\cfrac{1}{2}\cdot\cfrac{\sqrt{3}}{2}{a_k}^3=\cfrac{\sqrt{3}}{4}{a_k}^3$　・・・①

(2)より

$a_1=(\sqrt{6}-2)a_0$

でした。辺の長さが $a_1$ の正四面体を作った場合，$a_2$ と $a_1$ の関係もこれと同じになるはずです。よって

$a_{k+1}=(\sqrt{6}-2)a_k$

という漸化式を作ることができます。これは，初項 $a_0$，公比 $\sqrt{6}-2$ の等比数列です。

よって，一般項を求めると

$a_k=a_0(\sqrt{6}-2)^k$

もともと(2)で，$a_1=(\sqrt{6}-2)a_0$ だったので，$a_k=a_0(\sqrt{6}-2)^{k-1}$ としてしまうと，$a_1=a_0(\sqrt{6}-2)^0$ となってつじつまが合わないことになります。式がちゃんと成り立っているか確認してミスを減らしましょう。

これを①に代入すると
$V_k=\cfrac{\sqrt{3}}{4}{a_0}^3(\sqrt{6}-2)^{3k}$　（答え）

次に極限を求めましょう。

公比を見ると

$2<\sqrt{6}<3$
$0<\sqrt{6}-2<1$

だから，$k$ をどんどん大きくしていくと $(\sqrt{6}-2)^{3k}$ は 0 に収束していきます。

$V_k$ は初項 $\cfrac{\sqrt{3}}{4}{a_0}^3(\sqrt{6}-2)^3$，公比 $(\sqrt{6}-2)^3$ の等比数列です。

$\displaystyle\sum_{k=1}^\infty V_k$
$=\cfrac{\cfrac{\sqrt{3}}{4}{a_0}^3(\sqrt{6}-2)^3}{1-(\sqrt{6}-2)^3}$

あとは，ひたすら計算です。

$=\cfrac{\sqrt{3}}{4}{a_0}^3\cdot\cfrac{6\sqrt{6}-36+12\sqrt{6}-8}{1-(6\sqrt{6}-36+12\sqrt{6}-8)}$
$=\cfrac{\sqrt{3}}{4}{a_0}^3\cdot\cfrac{18\sqrt{6}-44}{45-18\sqrt{6}}$
$=\cfrac{\sqrt{3}}{4}{a_0}^3\cdot\cfrac{2(9\sqrt{6}-22)}{9(5-2\sqrt{6})}$
$=\cfrac{\sqrt{3}}{18}{a_0}^3\cdot\cfrac{9\sqrt{6}-22}{5-2\sqrt{6}}$

分母を有理化ます。

$=\cfrac{\sqrt{3}}{18}{a_0}^3\cdot\cfrac{(9\sqrt{6}-22)(5+2\sqrt{6})}{(5-2\sqrt{6})(5+2\sqrt{6})}$
$=\cfrac{\sqrt{3}}{18}{a_0}^3\cdot\cfrac{45\sqrt{6}+108-110-44\sqrt{6}}{25-24}$
$=\cfrac{\sqrt{3}(\sqrt{6}-2)}{18}{a_0}^3$
$=\cfrac{3\sqrt{2}-2\sqrt{3}}{18}{a_0}^3$　（答え）