2つの曲線に囲まれた領域の面積を求める(公式を使わない方法)(横浜国立大2018文系第3問)
$xy$ 平面上に放物線 $C_1:y=x^2$ と点 P$(p,q)$ $(q>p^2)$ があり,P を通り傾きが $t$ の直線を $\ell$ とする。さらに,$C_1$ と $\ell$ との 2 つの交点を結ぶ線分の中点において,放物線 $C_2:y=-x^2+ax+b$ が $\ell$ と接している。次の問いに答えよ。
(1) $a$,$b$ を求めよ。
(2) $C_1$ と $C_2$ で囲まれる領域の面積を求めよ。
(3) $t$ が実数全体を動くとき,(2)で求めた面積の最小値を求めよ。
条件を式に表す
(1)から始めます。
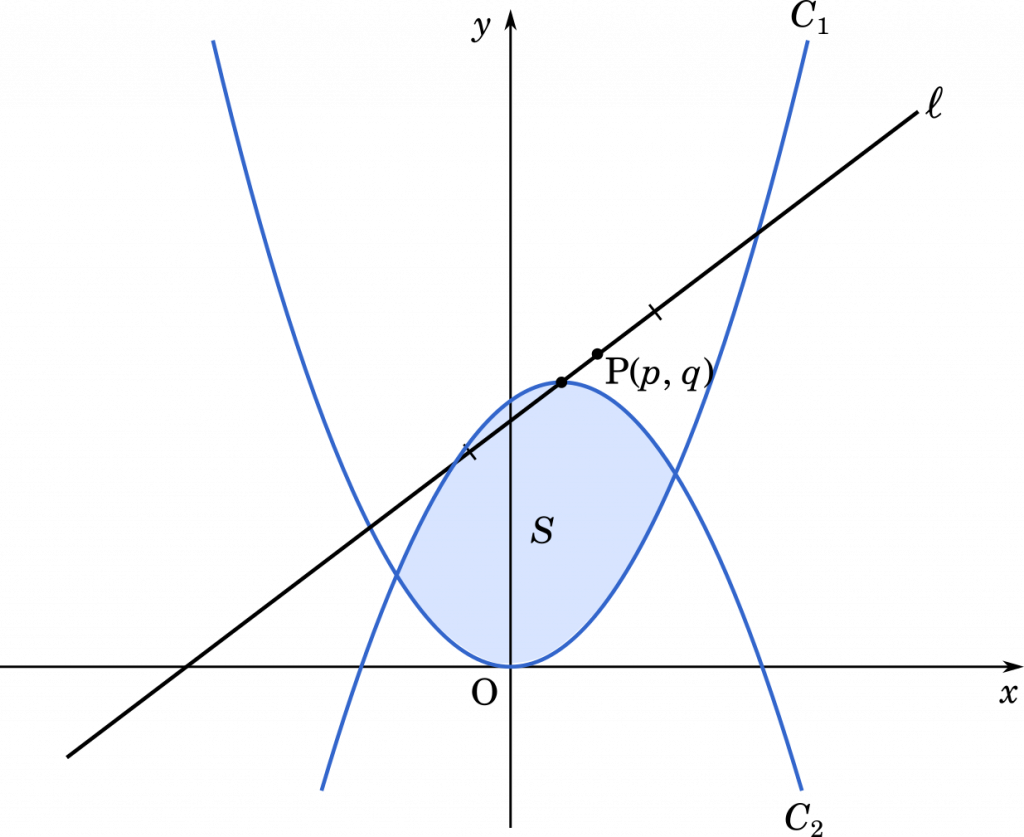


まずは,$\ell$ を数式で表しましょう。
$\ell$ は$(p,q)$ を通る 傾き $t$ の直線だから
$\ell:y-q=t(x-p)$
$y=tx-pt+q$
$C_1$ と $\ell$ が共通点を持つので
$x^2=tx-pt+q$
$x^2-tx+pt-q=0$
次に中点を考えます。方程式の解を $\alpha$,$\beta$ とすると中点の $x$ 座標は $\cfrac{\alpha+\beta}{2}$ です。
ここから,解と係数の関係を用いると良さそうです。
解と係数の関係より
$\alpha+\beta=t$
よって,中点の $x$ 座標は
$\cfrac{\alpha+\beta}{2}=\cfrac{t}{2}$
さらに,$\ell$ と $C_2$ は共通点を持つので
$tx-pt+q=-x^2+ax+b$
$x^2+(t-a)x-pt+q-b=0$
$x=\cfrac{t}{2}$ を代入すると
$\cfrac{t^2}{4}+\cfrac{t}{2}(t-a)-pt+q-b=0$
$t^2+2t^2-2at-4pt+4a-4b=0$ ・・・①
$\ell$ と $C_2$ は 1 点で接するので,判別式は
$D=(t-a)^2-4(-pt+q-b)=0$
$t^2-2at+a^2+4pt-4q+4b=0$ ・・・②
式を連立すると
①+②
$4t^2-4at+a^2=0$
$a^2-4at+4t^2=0$
$(a-2t)^2=0$
$a=2t$
①に代入して
$t^2+2t^2-4t^2-4pt+4q-4b=0$
$4b=-t^2-4pt+4q$
$b=q-pt-\cfrac{t^2}{4}$
したがって
$(a,b)=\Big(2t,q-pt-\cfrac{t^2}{4}\Big)$
2 つの曲線で囲まれた領域の面積
(2)に進みます。
2 つの曲線で囲まれた領域の面積を求めます。このパターンは受験テクニックとして公式が存在するのですが,ここでは公式を使わずに解いてみます。
面積を求めるには「上引く下」で考えるので,グラフの概形を描いて $C_2$ から $C_1$ を引いたものを積分することを確認しましょう。
$C_1$ と $C_2$ の交点を $\alpha$,$\beta$ $(\alpha<\beta)$ とすると
$\displaystyle S=\int_\alpha^\beta-x^2+ax+b-x^2\space dx$
$\displaystyle=\int_\alpha^\beta-2x^2+ax+b\space dx$
$=\Big[-\cfrac{2}{3}x^3+\cfrac{a}{2}x^2+bx\Big]_\alpha^\beta$
$=-\cfrac{2}{3}(\beta^3-\alpha^3)+\cfrac{a}{2}(\beta^2-\alpha^2)+b(\beta-\alpha)$
解と係数の関係を利用することを考えて,式を $\alpha+\beta$ と $\alpha\beta$ の形に持ち込みます。
$=-\cfrac{2}{3}(\beta-\alpha)(\beta^2+\alpha\beta+\alpha^2)+\cfrac{a}{2}(\alpha+\beta)(\beta-\alpha)+b(\beta-\alpha)$
$=(\beta-\alpha)\Big\{-\cfrac{2}{3}((\alpha+\beta)^2-\alpha\beta)+\cfrac{a}{2}(\alpha+\beta)+b\Big\}$
解と係数の関係を求めます。
$-2x^2+ax+b=0$ とすると
$\alpha+\beta=\cfrac{a}{2}$,$\alpha\beta=-\cfrac{b}{2}$
また
$(\beta-\alpha)^2=\alpha^2-2\alpha\beta+\beta^2$
$=(\alpha+\beta)^2-4\alpha\beta$
$=\cfrac{a^2}{4}+2b$
$\beta-\alpha=\sqrt{\cfrac{a^2}{4}+2b}$
これらを代入すると
$S=\sqrt{\cfrac{a^2}{4}+2b}\Big\{-\cfrac{2}{3}\Big(\cfrac{a^2}{4}+\cfrac{b}{2}\Big)+\cfrac{a^2}{4}+b\Big\}$
$S=\sqrt{\cfrac{a^2}{4}+2b}\Big(-\cfrac{a^2}{6}-\cfrac{b^2}{3}+\cfrac{a^2}{4}+b\Big)$
$S=\sqrt{\cfrac{a^2}{4}+2b}\Big(\cfrac{a^2}{12}+\cfrac{2}{3}b\Big)$
$S=\sqrt{\cfrac{a^2}{4}+2b}\cdot\cfrac{1}{3}\Big(\cfrac{a^2}{4}+2b\Big)$
$S=\cfrac{1}{3}\Big(\cfrac{a^2}{4}+2b\Big)^{\small{\frac{3}{2}}}$
$=\cfrac{1}{3}\Big(t^2+2q-2pt-\cfrac{t^2}{2}\Big)^{\small{\frac{3}{2}}}$
$=\cfrac{1}{3}\Big(\cfrac{t^2}{2}-2pt+2q\Big)^{\small{\frac{3}{2}}}$ (答え)
平方完成
(3)に進みます。
式を平方完成して最小値を求めましょう。
$S=\cfrac{1}{3}\Big(\cfrac{t^2}{2}-2pt+2q\Big)^{\small{\frac{3}{2}}}$ より
$f(t)=\cfrac{t^2}{2}-2pt+2q$ として,平方完成すると
$=\cfrac{1}{2}(t^2-4pt)+2q$
$=\cfrac{1}{2}(t-2p)^2-2p^2+2q$
よって,$f(t)$ の最小値は $-2p^2+2q$
したがって,最小値は
$\cfrac{1}{3}\Big(-2p^2+2q)^{\small{\frac{3}{2}}}$
$=\cfrac{1}{3}\cdot2^{\small{\frac{3}{2}}}\cdot\Big(q-p^2\Big)^{\small{\frac{3}{2}}}$
$=\cfrac{2\sqrt{2}}{3}(q-p^2)^{\small{\frac{3}{2}}}$ (答え)
SNSでシェア