区分求積の練習問題(横浜国立大2016理系第1問)

次の問いに答えよ。

(1) 関数 $f(x)=\cfrac{\log(1-x)}{x}$ は $0<x<1$ の範囲で減少することを示せ。

(2) 極限値

$\displaystyle\lim_{n\rightarrow\infty}\cfrac{1}{n}\sum_{k=1}^n\cfrac{1}{\tan\Bigg(\cfrac{(n+k)\pi}{6n}\Bigg)}$

を求めよ。

微分係数が負であることを示す

(1)から始めます。

先に理屈から言えば，式を微分して，微分係数がマイナスであることを示せば良いことになります。

分数だから，商の微分を使いましょう。

$f(x)=\cfrac{\log(1-x)}{x}$
$f'(x)=\cfrac{\{\log(1-x)\}’x-\log(1-x)(x)’}{x^2}$
$=\cfrac{\cfrac{1}{1-x}(-1)x-\log(1-x)}{x^2}$

分母と分子に $1-x$ をかけて式を整理します。

$=\cfrac{-x-(1-x)\log(1-x)}{x^2(1-x)}$

問われているのは，これが負の数になるのを示すことでした。分母の $x^2(1-x)$ は $0<x<1$ の範囲ではつねに正の数となるので，あとは分子が負の数であることを示しましょう。そのため，再び微分します。今度はかけ算の微分の公式を使いましょう。

$g(x)=-x-(1-x)\log(1-x)$ として
$g'(x)=-1-\Big\{-\log(1-x)-(1-x)\cfrac{1}{x-1}\Big\}$
$=-1+\log(1-x)+1$
$=\log(1-x)<0$

よって，$g(x)$ は $0<x<1$ で単調に減少する。したがって，$f'(x)$ は負の値となるので，$f(x)$ は単調に減少する。（証明終わり）

区分求積

(2)に進みます。

極限と総和の組み合わせを見たときに，区分求積を使うことがピンと来るようになりましょう。

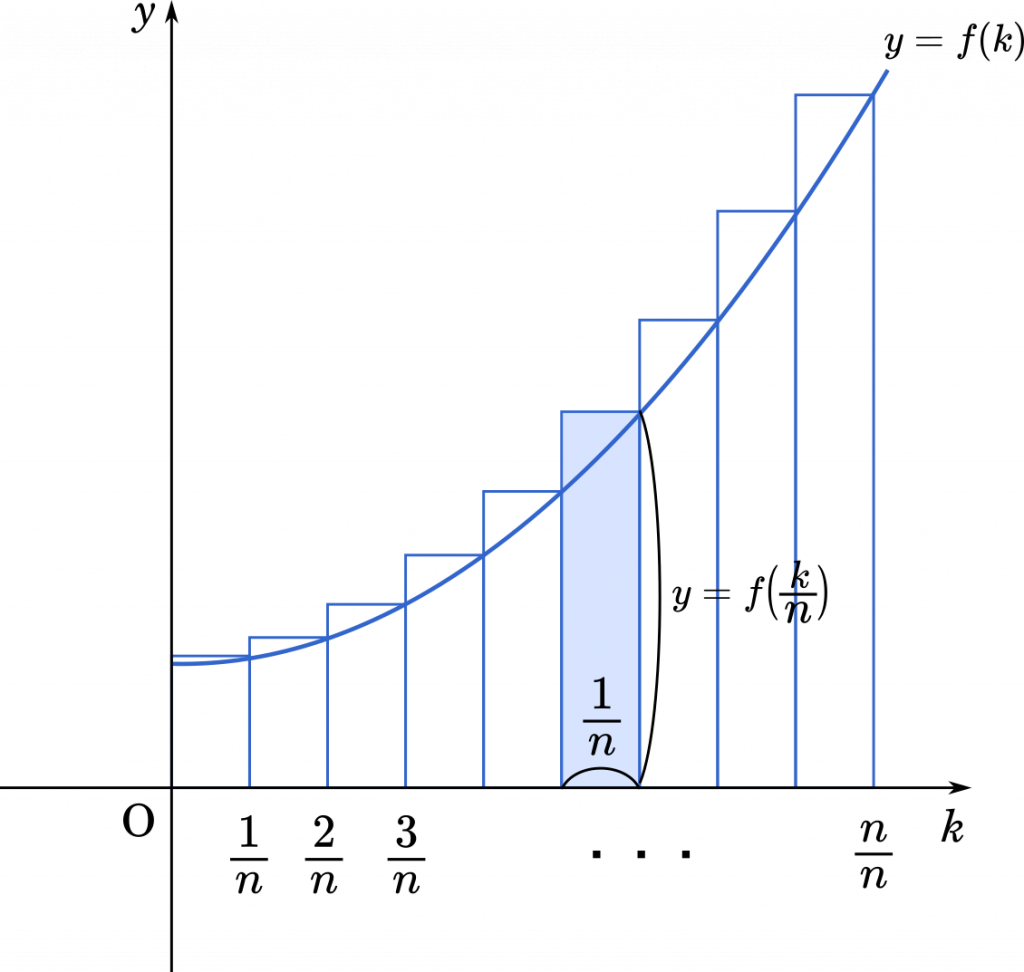
ざっくりイメージで言えば長方形の面積を足し合わせていくのが区分求積でした。長方形のヨコの長さを $\cfrac{1}{n}$，タテの長さを $f\Big(\cfrac{k}{n}\Big)$ として，$k=1,2,3,\cdots$ の面積を足し合わせると

$\displaystyle\cfrac{1}{n}\times f\Big(\cfrac{1}{n}\Big)+\cfrac{1}{n}\times f\Big(\cfrac{2}{n}\Big)+\cfrac{1}{n}\times f\Big(\cfrac{3}{n}\Big)+\cdots+\cfrac{1}{n}\times f\Big(\cfrac{n}{n}\Big)=\cfrac{1}{n}\sum_{k=1}^nf\Big(\cfrac{k}{n}\Big)$

一番最後の $k$ の値は，$\cfrac{n}{n}=1$ なので，区間は $[0,1]$ ということになります。この状態では，$[0,1]$ の区間を $n$ 個で分割していることになります。あとは，$n$ 個の区切りを限りなく細かくしていけば，$f(x)$ の積分の結果に限りなく近づいていくという仕組みです。

計算のおおまかなイメージをつかみながら公式を覚えると，忘れにくくなると思います。

$\displaystyle\lim_{n\rightarrow\infty}\cfrac{1}{n}\sum_{k=1}^n\cfrac{1}{\tan\bigg(\cfrac{(n+k)\pi}{6n}\bigg)}$

このままでは積分に置き換えはできません。公式を見れば分かる通り，$k$ の部分を $\cfrac{k}{n}$ という形にしなければなりません。

$\displaystyle=\lim_{n\rightarrow\infty}\cfrac{1}{n}\sum_{k=1}^n\cfrac{1}{\tan\Bigg(\cfrac{(1+\cfrac{k}{n})\pi}{6}\Bigg)}$

あとは $\cfrac{k}{n}$ の部分を $x$ に置きかえれば積分の式になります。

$\displaystyle=\int_0^1\cfrac{1}{\tan\bigg(\cfrac{(1+x)\pi}{6}\bigg)}\space dx$

$\tan$ を積分するときには，$\tan\theta=\cfrac{\sin\theta}{\cos\theta}$ に変形します。ここでは，$\cfrac{1}{\tan\theta}=\cfrac{\cos\theta}{\sin\theta}$ です。

$\displaystyle=\int_0^1\cfrac{\cos\bigg(\cfrac{(1+x)\pi}{6}\bigg)}{\sin\bigg(\cfrac{(1+x)\pi}{6}\bigg)}\space dx$

$\displaystyle=\cfrac{6}{\pi}\bigg[\log\bigg\{\sin\bigg(\cfrac{(1+x)\pi}{6}\bigg)\bigg\}\bigg]_0^1$

$\log$ の微分は $(\log x)’=\cfrac{1}{x}$ でした。そして，上の式は合成関数なので，$\sin$ を微分したものをかける必要があります。そして $\sin\bigg(\cfrac{(1+x)\pi}{6}\bigg)$ 自体もまた合成関数なので，$\cfrac{(1+x)\pi}{6}$ を微分したものをかけるという流れです。

$\cfrac{6}{\pi}\log\bigg\{\sin\bigg(\cfrac{(1+x)\pi}{6}\bigg)\bigg\}$ を微分すると

$\cfrac{6}{\pi}\cdot\cfrac{1}{\sin\bigg(\cfrac{(1+x)\pi}{6}\bigg)}\cdot\cos\bigg(\cfrac{(1+x)\pi}{6}\bigg)\cdot\cfrac{(0+1)\pi}{6}$
$=\cfrac{\cos\bigg(\cfrac{(1+x)\pi}{6}\bigg)}{\sin\bigg(\cfrac{(1+x)\pi}{6}\bigg)}$

となって，もとの式に戻ります。$\log\bigg\{\sin\bigg(\cfrac{(1+x)\pi}{6}\bigg)\bigg\}$ を微分すると $\cfrac{\pi}{6}$ という余計な部分が出てくるので，$\cfrac{6}{\pi}$ をかけて帳尻合わせをするという仕組みです。

$=\cfrac{6}{\pi}\Big\{\log\Big(\sin\cfrac{2\pi}{3}\Big)-\log\Big(\sin\cfrac{\pi}{6}\Big)\Big\}$
$=\cfrac{6}{\pi}\Big(\log\cfrac{\sqrt{3}}{2}-\log\cfrac{1}{2}\Big)$
$=\cfrac{6}{\pi}\Bigg(\log\cfrac{\cfrac{\sqrt{3}}{2}}{\cfrac{1}{2}}\Bigg)$
$=\cfrac{6}{\pi}\log\sqrt{3}$
$=\cfrac{6}{\pi}\log3^{\small{\frac{1}{2}}}$
$=\cfrac{3}{\pi}\log3$　（答え）