移動する直線が示す領域とその面積を求める コツは x を固定すること(横浜国立大2019理系第4問)
O を原点とする $xy$ 平面上に 2 点 A$(2,0)$,B$(0,2)$ がある。2 点 P,Q は条件(*)をみたしながら動く。
(*)$\begin{cases}\textsf{Pは線分OA上にある。}\\\textsf{Qは線分OA上にある。}\\\textsf{△OPQの面積は 1 である。}\end{cases}$
点 P の座標を $(t,0)$ とする。次の問いに答えよ。
(1) $t$ のとり得る値の範囲を求めよ。
(2) $t$ が(1)で求めた範囲を動くとき,線分 PQ が通過する領域を $xy$ 平面上に図示せよ。
(3) (2)で求めた領域の面積 $S$ を求めよ。
t の範囲を求める
(1)から始めます。

Q$(0,s)$ とおくと
△OPQ$=\cfrac{1}{2}ts=1$
$s=\cfrac{2}{t}$
これは反比例のグラフです。
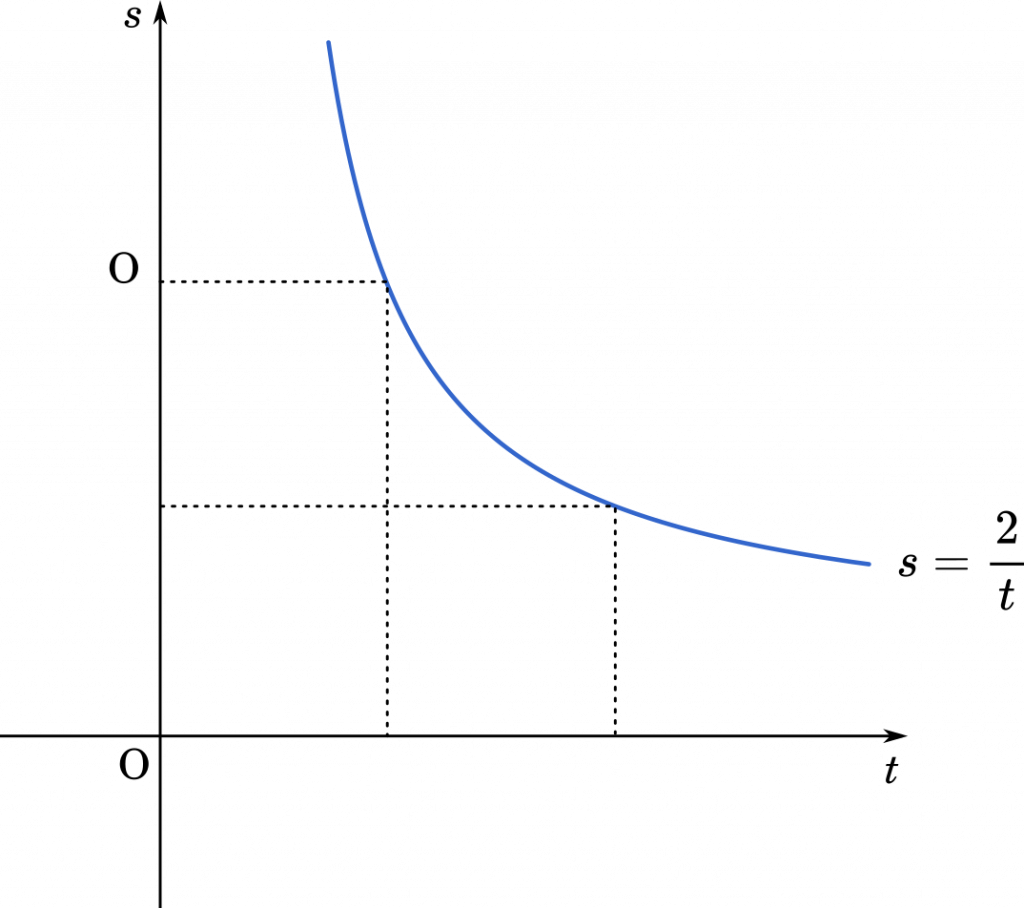
$t$ と $s$ はともに 2 を超えることができないので,グラフを描いてみると $t$ のとり得る範囲が見えてきます。
したがって
$1\leqq t\leqq2$ (答え)
移動する直線がつくる領域
(2)に進みます。
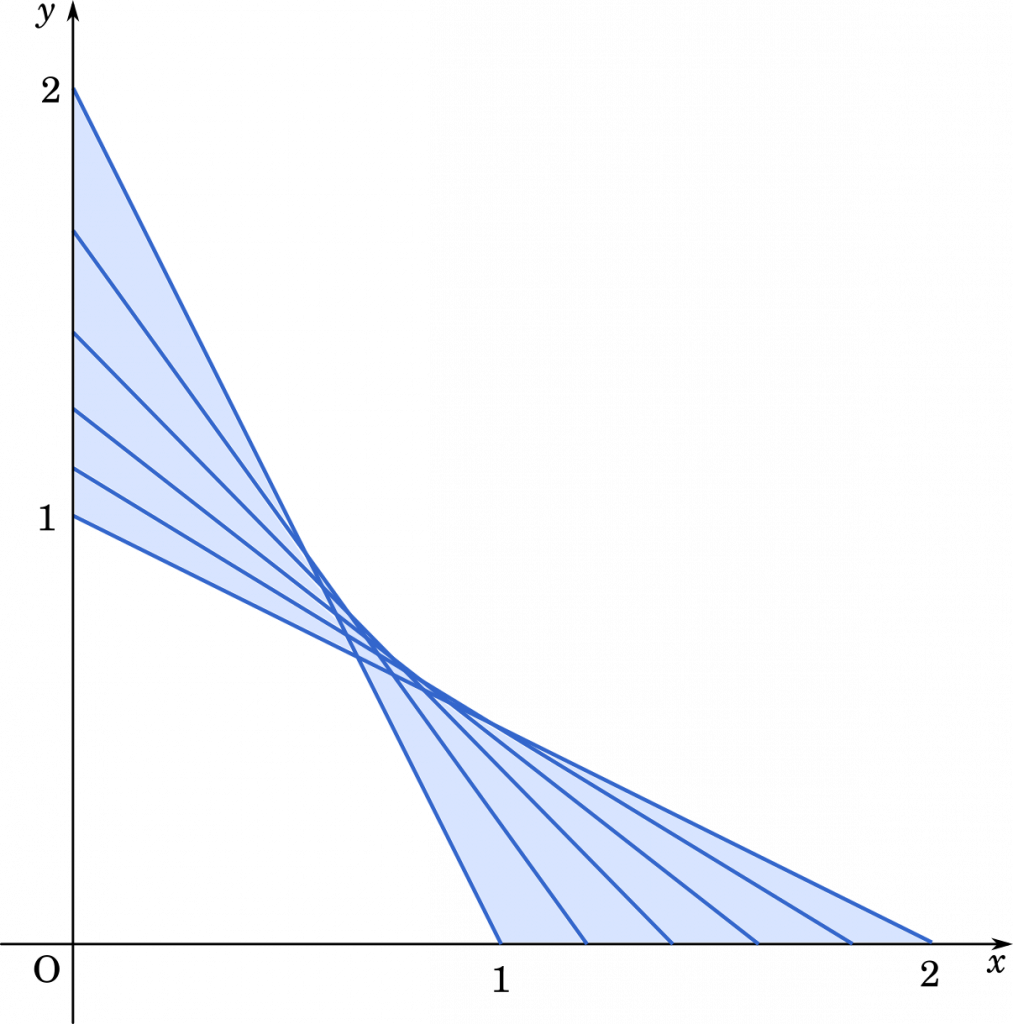
領域を図示すること自体はそれほど難しくなく,上のようになります。
あとはこれを式の形で示しましょう。
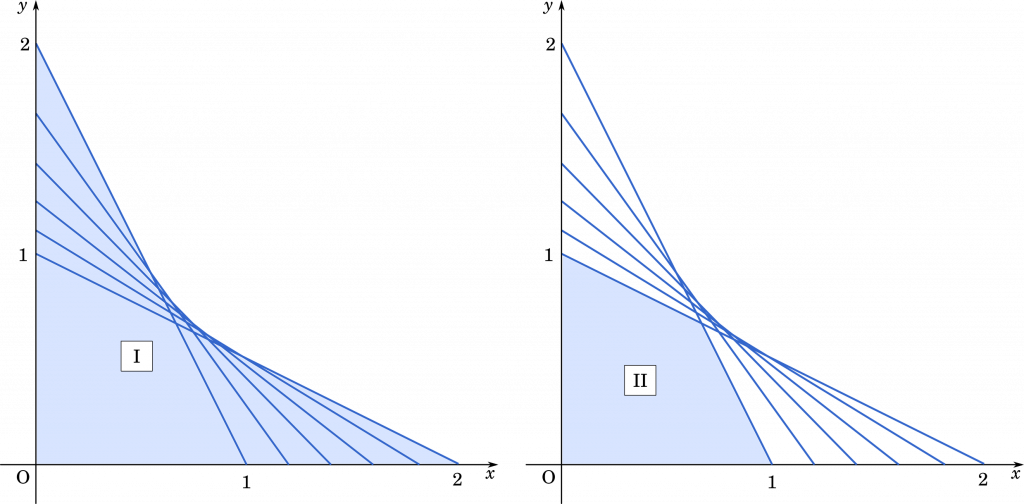
まず,領域 I について考えてみます。
(1)より
$t=\cfrac{2}{s}$
$s=\cfrac{2}{t}$
となる。P$(t,0)$,Q$\Big(0,\cfrac{2}{t}\Big)$ を通る直線の式は
$y=-\cfrac{\space\cfrac{2}{t}\space}{t}\space x+\cfrac{2}{t}$
$=-\cfrac{2}{t^2}x+\cfrac{2}{t}$
よって,領域 I は
$y\leqq-\cfrac{2}{t^2}x+\cfrac{2}{t}$


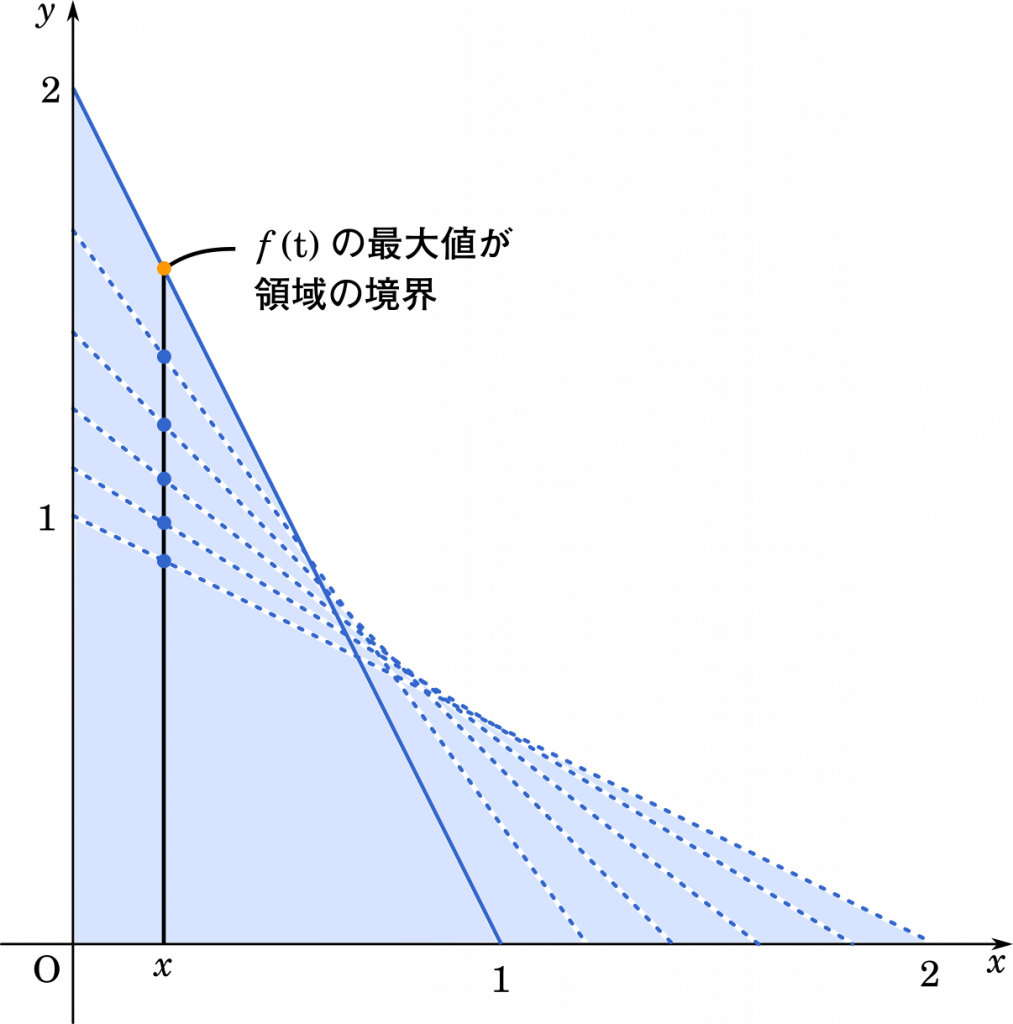
そこで,いったん式を $f(x)$ ではなく $f(t)$ とします。このとき,$t$ を変化する値と考え,$x$ はある決まった値(定数)であると考えます。そうすると,この関数は $t$ の値によって $f(t)$ の値($y$ の値)が変わり,タテ方向に垂直に移動することになります。
こうして,上のグラフを見てみると,$f(t)$ の最大値が領域の境界であるが分かります。
微分して最大値を求めてみましょう。
$f(t)=-\cfrac{2}{t^2}x+\cfrac{2}{t}$ とすると
$f(t)=-2t^{-2}x+2t^{-1}$
微分して
$f'(t)=4t^{-3}x-2t^{-2}$
$=\cfrac{4}{t^3}x-\cfrac{2}{t^2}$
$\cfrac{4}{t^3}x-\cfrac{2}{t^2}=0$ とすると
(1)より $t\not=0$ だから,両辺に $t^3$ をかけると
$4x-2t=0$
$t=2x$ $(x\geqq0)$
増減表は
$\def\arraystretch{1.5}\begin{array}{|c|c|c|c|c|}\hline t&(0)&\cdots&2x&\cdots\\\hline f'(t)&&+&0&-\\\hline f(t)&&\nearrow&&\searrow\\\hline\end{array}$





(i) $0\leqq x\leqq\cfrac{1}{2}$ のとき,$t=1$ で最大
$f(1)=-2x+2$
(ii) $\cfrac{1}{2}<x\leqq1$ のとき,$t=2x$ で最大
$f(2x)=-\cfrac{2}{4x^2}x+\cfrac{2}{2x}$
$=-\cfrac{1}{2x}+\cfrac{1}{x}$
$=\cfrac{1}{2x}$
これは,反比例のグラフになります。
(iii) $1<x\leqq2$ のとき,$t=2$ で最大
$f(2)=-\cfrac{2}{4}x+\cfrac{2}{2}$
$=-\cfrac{1}{2}x+1$
したがって,領域 I は
領域 I $\begin{cases}y\leqq-2x+2\space\Big(0\leqq x<\cfrac{1}{2}\Big)\\y\leqq\cfrac{1}{2x}\space\Big(\cfrac{1}{2}<x\leqq1\Big)\\y\leqq-\cfrac{1}{2}x+1\space(1<x\leqq2)\end{cases}$
また,$x=\cfrac{1}{2}$ のとき $y=-2x+2$ に代入して
$y=-2\cdot\cfrac{1}{2}+2$
$=1$
$x=1$ のとき $y=\cfrac{1}{2x}$ に代入して
$y=\cfrac{1}{2}$
次に,領域 II について考えます。
領域 II は $(1,0)$ と $(0,2)$ を通る直線,および $(2,0)$ と $(0,1)$ を通る直線だから
$y=-\cfrac{1}{2}x+1$
$y=-2x+2$
で囲まれた部分です。
交点を求めておきましょう。
式を連立して
$-\cfrac{1}{2}x+1=-2x+2$
$-x+2=-4x+4$
$3x=2$
$x=\cfrac{2}{3}$
よって
$y=-2\cdot\cfrac{2}{3}+2=\cfrac{2}{3}$
交点の座標は $\Big(\cfrac{2}{3},\space\cfrac{2}{3}\Big)$
したがって,領域 II は
領域II $\begin{cases}y\geqq-\cfrac{1}{2}x+1\space\Big(0\leqq x<\cfrac{2}{3}\Big)\\y\geqq-2x+2\space\Big(\cfrac{2}{3}<x\leqq1\Big)\end{cases}$
領域 I,II を重ねると
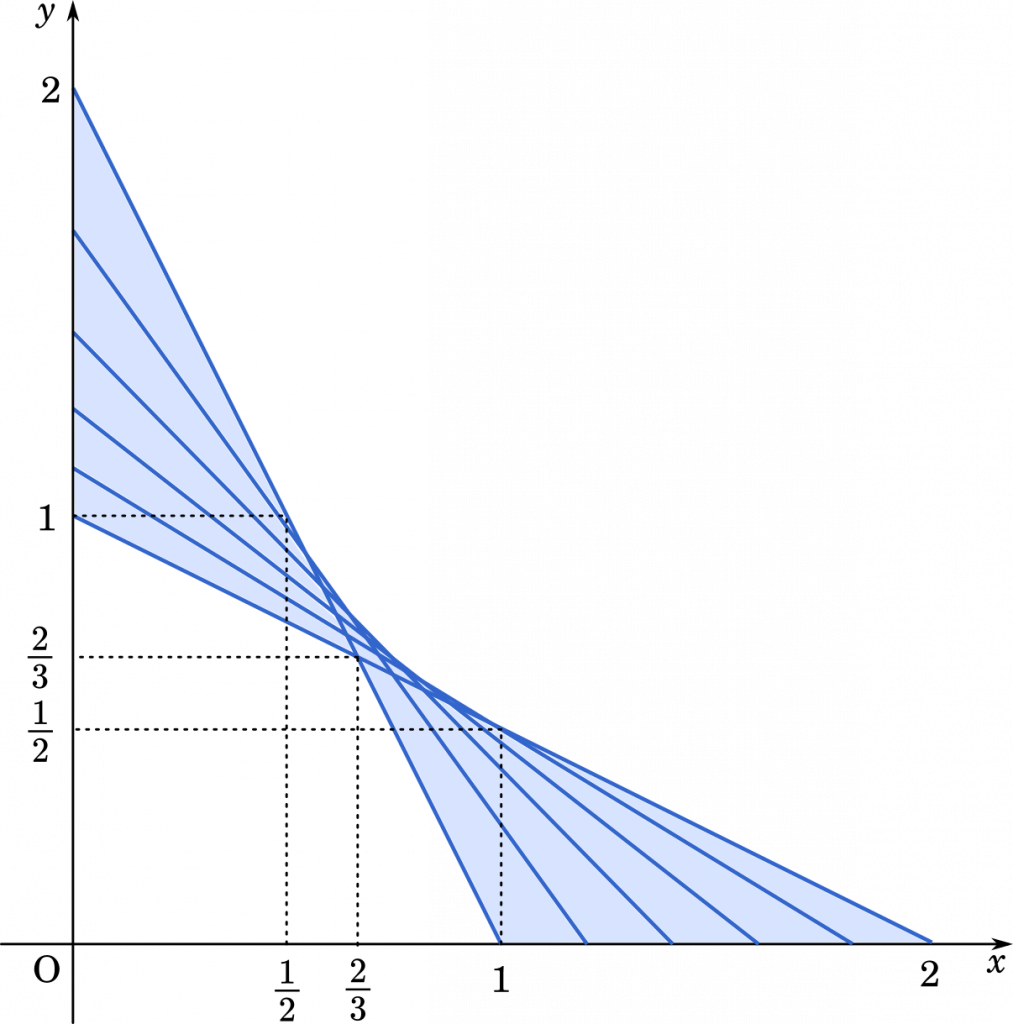
(答え)
領域の面積
(3)に進みます。
面積は (2) で求めた領域 I から領域 II を引けば求められます。あとは,図形を台形や三角形などに分解して計算していきましょう。
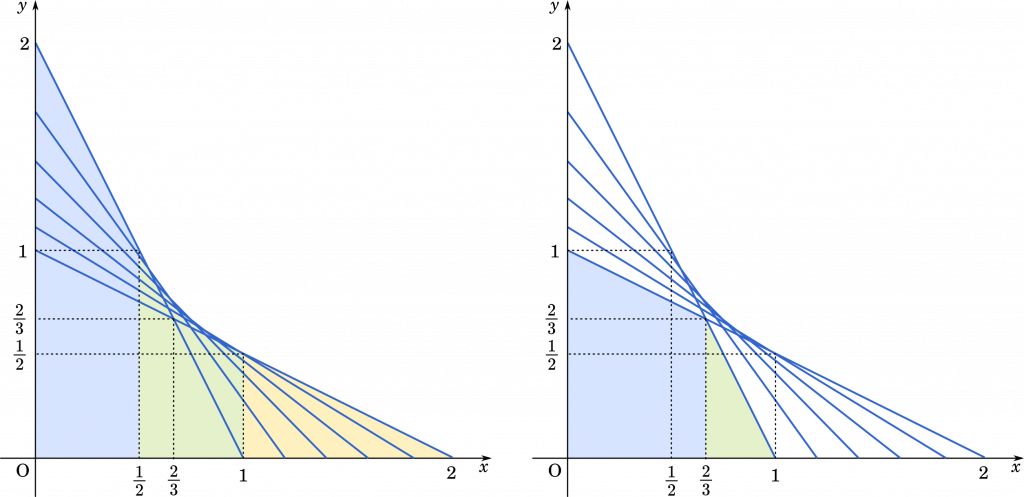
$\displaystyle S=\cfrac{1}{2}(2+1)\cdot\cfrac{1}{2}+\int_{\small{\frac{1}{2}}}^1\cfrac{1}{2x}\space dx+\cfrac{1}{2}\cdot1\cdot\cfrac{1}{2}-\cfrac{1}{2}\Big(1+\cfrac{2}{3}\Big)\cdot\cfrac{2}{3}-\cfrac{1}{2}\cdot\cfrac{1}{3}\cdot\cfrac{2}{3}$
$=\cfrac{3}{4}+\cfrac{1}{2}\Big[\log 2x\Big]_{\small{\frac{1}{2}}}^1+\cfrac{1}{4}-\cfrac{5}{9}-\cfrac{1}{9}$
$=\cfrac{1}{3}+\cfrac{1}{2}(\log2-\log1)$
$=\cfrac{1}{3}+\cfrac{1}{2}\log 2$ (答え)
移動する直線が重なることによって領域を作るパターンは決して珍しいものではないので,マスターしましょう。コツは $x$ の値を固定して $t$ を変化させ,$y$ の最大値を求めることでした。グラフを見ながらイメージをつかみましょう。
SNSでシェア