対数関数の式を t に置き換えて整理する(東京都立大2020文系第1問)
$a$ を実数とする。関数 $f(x)$ を
$f(x)=\cfrac{1}{4}(\log_{\small{\frac{1}{2}}}x^2)^2-\log_{\small{\frac{1}{2}}}(8x^{1-a})+a-8$ $(1\leqq x\leqq4)$
と定める。$t=\log_{\small{\frac{1}{2}}}x$ とおくとき,以下の問いに答えなさい。
(1) $f(x)$ を $t$ を用いて表しなさい。
(2) $1\leqq x\leqq4$ のとき,$t$ の値の範囲を求めなさい。
(3) 次の条件(*)をみたす $a$ の値の範囲を求めなさい。
(*)$1\leqq x\leqq4$ のとき,$f(x)<0$ である。
対数関数の整理
(1)から始めます。
$f(x)=\cfrac{1}{4}(2\log_{\small{\frac{1}{2}}}x)^2-(\log_{\small{\frac{1}{2}}}8+\log_{\small{\frac{1}{2}}}x^{1-a})+a-8$


次に,$\log_{\small{\frac{1}{2}}}8$ の値を考えてみましょう。これは,$\cfrac{1}{2}$ を何乗したら 8 になる?ということです。


よって
$=\cfrac{1}{4}(2t)^2-\{-3+(1-a)\log_{\small{\frac{1}{2}}}x\}+a-8$
$=t^2+3-(1-a)t+a-8$
$=t^2-(1-a)t+a-5$ (答え)
t の範囲を求める
(2)に進みます。
$\log_{\small{\frac{1}{2}}}1=0$
$\log_{\small{\frac{1}{2}}}4=-2$
したがって
$-2\leqq t\leqq0$ (答え)
値が負になる場合を考える
(3)に進みます。
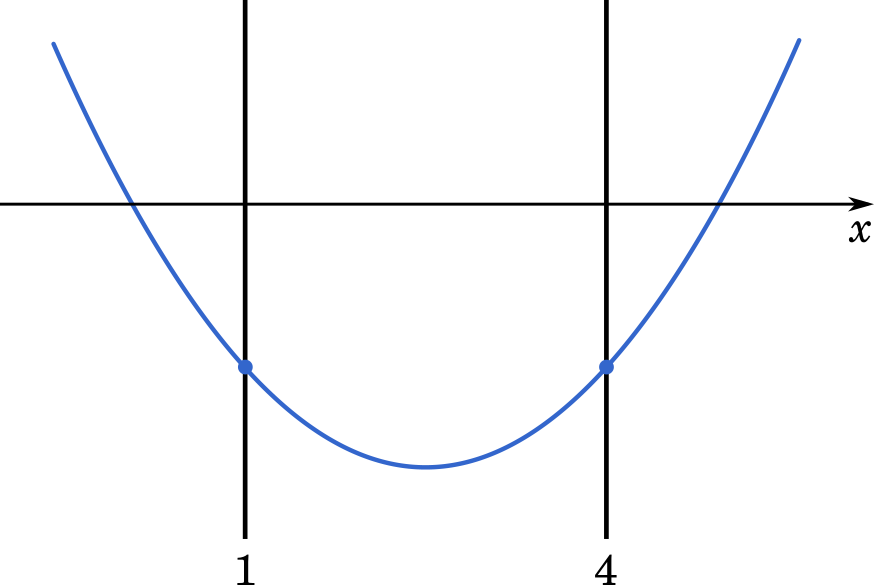
$f(x)$ は下に凸のグラフなので,$f(1)<0$ かつ $f(4)<0$ であれば,$1\leqq x\leqq4$ の区間において,$f(x)$ はつねに負の値であると言えます。
(1) より $f(x)=t^2-(1-a)t+a-5$ とする。
(2)より,$x=1$ のとき $t=0$ だから
$f(1)=a-5<0$
$a<5$
また
$x=4$ のとき $t=-2$ だから
$f(4)=(-2)^2-(1-a)(-2)+a-5$
$=4+2-2a+a-5$
$=-a+1$
$-a+1<0$
$a>1$
したがって
$1<a<5$ (答え)
SNSでシェア