O を原点とする座標平面の x x x x x x π 3 \cfrac{\pi}{3} 3 π π 4 \cfrac{\pi}{4} 4 π
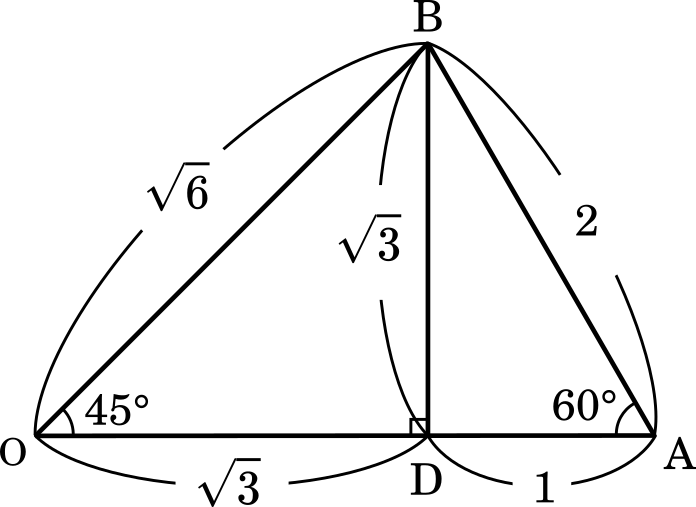
(1) 線分 OA,OB の長さを求めなさい。
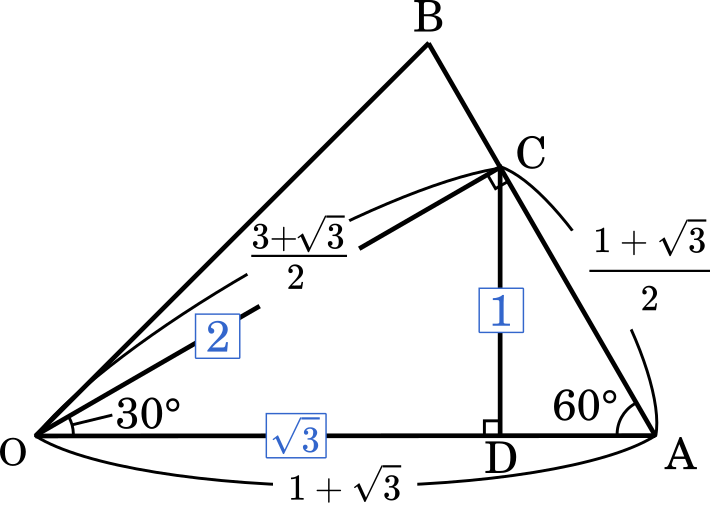
(2) 点 C の座標を求めなさい。
(3) 実数 t t t 0 < t < 1 0<t<1 0 < t < 1 t : ( 1 − t ) t:(1-t) t : ( 1 − t ) P t \text{P}_t P t ( 1 − t ) : t (1-t):t ( 1 − t ) : t Q t \text{Q}_t Q t OP t → ⋅ OQ t → \overrightarrow{\text{OP}_t}\cdot\overrightarrow{\text{OQ}_t} OP t ⋅ OQ t t t t
三角比から辺の長さを求める
(1)から始めます。
ここは計算式を立てるより,辺の比が 1 : 2 : 3 1:2:\sqrt{3} 1 : 2 : 3 1 : 1 : 2 1:1:\sqrt{2} 1 : 1 : 2
OA=1 + 3 1+\sqrt{3} 1 + 3 6 \sqrt{6} 6
さらに三角比を用いる
(2)に進みます。
これも(1)と同じで,△OAC は辺の比が 1 : 2 : 3 1:2:\sqrt{3} 1 : 2 : 3 1 + 3 1+\sqrt{3} 1 + 3
OA=1 + 3 1+\sqrt{3} 1 + 3
OA:OC=2 : 3 2:\sqrt{3} 2 : 3
OC=3 2 \cfrac{\sqrt{3}}{2} 2 3 = 3 2 ( 1 + 3 ) =\cfrac{\sqrt{3}}{2}(1+\sqrt{3}) = 2 3 ( 1 + 3 ) = 3 + 3 2 =\cfrac{3+\sqrt{3}}{2} = 2 3 + 3
よって
OC:CD=2 : 1 2:1 2 : 1 1 2 \cfrac{1}{2} 2 1 = 1 2 ⋅ 3 + 3 2 =\cfrac{1}{2}\cdot\cfrac{3+\sqrt{3}}{2} = 2 1 ⋅ 2 3 + 3 = 3 + 3 4 =\cfrac{3+\sqrt{3}}{4} = 4 3 + 3
また
OC:OD=2 : 3 2:\sqrt{3} 2 : 3 3 2 \cfrac{\sqrt{3}}{2} 2 3 = 3 2 ⋅ 3 + 3 2 =\cfrac{\sqrt{3}}{2}\cdot\cfrac{3+\sqrt{3}}{2} = 2 3 ⋅ 2 3 + 3 = 3 + 3 3 4 =\cfrac{3+3\sqrt{3}}{4} = 4 3 + 3 3
したがって,点 C の座標は
( 3 + 3 3 4 , 3 + 3 4 ) \Big(\cfrac{3+3\sqrt{3}}{4},\cfrac{3+\sqrt{3}}{4}\Big) ( 4 3 + 3 3 , 4 3 + 3 )
平方完成して最小値を求める
(3)に進みます。
ここは内分点を求め,そこから内積を求めます。作業は難しくないので,地道に計算式を作っていきましょう。
内分点の式は
OP t → = ( 1 − t ) OA → + t OB → \overrightarrow{\text{OP}_t}=(1-t)\overrightarrow{\text{OA}}+t\overrightarrow{\text{OB}} OP t = ( 1 − t ) OA + t OB OQ t → = t OC → + ( 1 − t ) OD → \overrightarrow{\text{OQ}_t}=t\overrightarrow{\text{OC}}+(1-t)\overrightarrow{\text{OD}} OQ t = t OC + ( 1 − t ) OD
内積の式は
OP t → ⋅ OQ t → = { ( 1 − t ) OA → + t OB → } { t OC → + ( 1 − t ) OD → } \overrightarrow{\text{OP}_t}\cdot\overrightarrow{\text{OQ}_t}=\{(1-t)\overrightarrow{\text{OA}}+t\overrightarrow{\text{OB}}\}\{t\overrightarrow{\text{OC}}+(1-t)\overrightarrow{\text{OD}}\} OP t ⋅ OQ t = {( 1 − t ) OA + t OB } { t OC + ( 1 − t ) OD } = ( t − t 2 ) OA → ⋅ OC → + ( 1 − t ) 2 OA → ⋅ OD → + t 2 OB → ⋅ OC → + ( t − t 2 ) OB → ⋅ OD → =(t-t^2)\overrightarrow{\text{OA}}\cdot\overrightarrow{\text{OC}}+(1-t)^2\overrightarrow{\text{OA}}\cdot\overrightarrow{\text{OD}}+t^2\overrightarrow{\text{OB}}\cdot\overrightarrow{\text{OC}}+(t-t^2)\overrightarrow{\text{OB}}\cdot\overrightarrow{\text{OD}} = ( t − t 2 ) OA ⋅ OC + ( 1 − t ) 2 OA ⋅ OD + t 2 OB ⋅ OC + ( t − t 2 ) OB ⋅ OD
OA → = ( 1 + 3 , 0 ) \overrightarrow{\text{OA}}=(1+\sqrt{3},0) OA = ( 1 + 3 , 0 ) OB → = ( 3 , 3 ) \overrightarrow{\text{OB}}=(\sqrt{3},\sqrt{3}) OB = ( 3 , 3 ) OC → = ( 3 + 3 4 , 3 + 3 4 ) \overrightarrow{\text{OC}}=\Big(\cfrac{3+\sqrt{3}}{4},\cfrac{3+\sqrt{3}}{4}\Big) OC = ( 4 3 + 3 , 4 3 + 3 ) OD → = ( 3 , 0 ) \overrightarrow{\text{OD}}=(\sqrt{3},0) OD = ( 3 , 0 )
よって
OA → ⋅ OC → = ( 1 + 3 ) ⋅ 3 + 3 3 4 + 3 ⋅ 3 + 3 4 \overrightarrow{\text{OA}}\cdot\overrightarrow{\text{OC}}=(1+\sqrt{3})\cdot\cfrac{3+3\sqrt{3}}{4}+\sqrt{3}\cdot\cfrac{3+\sqrt{3}}{4} OA ⋅ OC = ( 1 + 3 ) ⋅ 4 3 + 3 3 + 3 ⋅ 4 3 + 3 = 1 4 ( 3 3 + 9 + 3 3 + 3 ) =\cfrac{1}{4}(3\sqrt{3}+9+3\sqrt{3}+3) = 4 1 ( 3 3 + 9 + 3 3 + 3 ) = 1 4 ( 12 + 6 3 ) =\cfrac{1}{4}(12+6\sqrt{3}) = 4 1 ( 12 + 6 3 ) = 3 + 3 3 2 =3+\cfrac{3\sqrt{3}}{2} = 3 + 2 3 3 OA → ⋅ OD → = 3 ( 1 + 3 ) = 3 + 3 \overrightarrow{\text{OA}}\cdot\overrightarrow{\text{OD}}=\sqrt{3}(1+\sqrt{3})=3+\sqrt{3} OA ⋅ OD = 3 ( 1 + 3 ) = 3 + 3 OB → ⋅ OC → = 3 ⋅ 3 + 3 3 4 + 3 ⋅ 3 + 3 4 \overrightarrow{\text{OB}}\cdot\overrightarrow{\text{OC}}=\sqrt{3}\cdot\cfrac{3+3\sqrt{3}}{4}+\sqrt{3}\cdot\cfrac{3+\sqrt{3}}{4} OB ⋅ OC = 3 ⋅ 4 3 + 3 3 + 3 ⋅ 4 3 + 3 = 1 4 ( 3 3 + 9 + 3 3 + 3 ) =\cfrac{1}{4}(3\sqrt{3}+9+3\sqrt{3}+3) = 4 1 ( 3 3 + 9 + 3 3 + 3 ) = 1 4 ( 12 + 6 3 ) = 3 + 3 3 2 =\cfrac{1}{4}(12+6\sqrt{3})=3+\cfrac{3\sqrt{3}}{2} = 4 1 ( 12 + 6 3 ) = 3 + 2 3 3 OB → ⋅ OD → = 3 ⋅ 3 = 3 \overrightarrow{\text{OB}}\cdot\overrightarrow{\text{OD}}=\sqrt{3}\cdot\sqrt{3}=3 OB ⋅ OD = 3 ⋅ 3 = 3
①に代入すると
OP t → ⋅ OQ t → = ( t − t 2 ) ( 3 + 3 3 2 ) + ( 1 − 2 t + t 2 ) ( 3 + 3 ) + t 2 ( 3 + 3 3 2 ) + ( t − t 2 ) ⋅ 3 \overrightarrow{\text{OP}_t}\cdot\overrightarrow{\text{OQ}_t}=(t-t^2)\Big(3+\cfrac{3\sqrt{3}}{2}\Big)+(1-2t+t^2)(3+\sqrt{3})+t^2\Big(3+\cfrac{3\sqrt{3}}{2}\Big)+(t-t^2)\cdot3 OP t ⋅ OQ t = ( t − t 2 ) ( 3 + 2 3 3 ) + ( 1 − 2 t + t 2 ) ( 3 + 3 ) + t 2 ( 3 + 2 3 3 ) + ( t − t 2 ) ⋅ 3 = 3 t + 3 3 2 t − 3 t 2 − 3 3 2 t 2 + 3 − 6 t + 3 t 2 + 3 − 2 3 t + 3 t 2 + 3 t 2 + 3 3 2 t 2 + 3 t − 3 t 2 =3t+\cfrac{3\sqrt{3}}{2}t-3t^2-\cfrac{3\sqrt{3}}{2}t^2+3-6t+3t^2+\sqrt{3}-2\sqrt{3}t+\sqrt{3}t^2+3t^2+\cfrac{3\sqrt{3}}{2}t^2+3t-3t^2 = 3 t + 2 3 3 t − 3 t 2 − 2 3 3 t 2 + 3 − 6 t + 3 t 2 + 3 − 2 3 t + 3 t 2 + 3 t 2 + 2 3 3 t 2 + 3 t − 3 t 2 = 3 t 2 − 3 2 t + 3 + 3 =\sqrt{3}t^2-\cfrac{\sqrt{3}}{2}t+3+\sqrt{3} = 3 t 2 − 2 3 t + 3 + 3
最小値を求めるために,式を平方完成します。
= 3 ( t 2 − 1 2 t ) + 3 + 3 =\sqrt{3}\Big(t^2-\cfrac{1}{2}t\Big)+3+\sqrt{3} = 3 ( t 2 − 2 1 t ) + 3 + 3 = 3 ( t − 1 4 ) 2 − 3 16 + 3 + 3 =\sqrt{3}\Big(t-\cfrac{1}{4}\Big)^2-\cfrac{\sqrt{3}}{16}+3+\sqrt{3} = 3 ( t − 4 1 ) 2 − 16 3 + 3 + 3 = 3 ( t − 1 4 ) 2 + 3 + 15 3 16 =\sqrt{3}\Big(t-\cfrac{1}{4}\Big)^2+3+\cfrac{15\sqrt{3}}{16} = 3 ( t − 4 1 ) 2 + 3 + 16 15 3
したがって
最小値は t = 1 4 t=\cfrac{1}{4} t = 4 1 3 + 15 3 16 3+\cfrac{15\sqrt{3}}{16} 3 + 16 15 3
関連