二次方程式の解と係数の関係が成り立つ仕組みをおさらい／解が三角関数のとき(東京都立大2017文系第1問)

たとえば，$x^2-2x-3=0$ という方程式は，因数分解して
$(x+1)(x-3)=0$
$x=-1,\space3$
となります。つまり，カッコの中の 1 と 3 の部分が解になっているということです。
ここで，解を $\alpha,\space\beta$ とするなら
$(x-\alpha)(x-\beta)=0$
となります。
ここで大事なポイントですが，どんな二次方程式でも 2 つの解を用いて $(x-\alpha)(x-\beta)=0$ という式を作ることができます。

$(x-\alpha)(x-\beta)$ を展開してみましょう。
$x^2-(\alpha+\beta)x+\alpha\beta=0$
もし，$\alpha=-1$ で $\beta=3$ なら
$x^2-(-1+3)x+(-1)\times3=0$
$x^2-2x-3=0$
となり，最初の式に戻りました。

いったん，
$\alpha+\beta=-\cfrac{b}{a}$
$\alpha\beta=\cfrac{c}{a}$
とします。これを $x^2-(\alpha+\beta)x+\alpha\beta=0$ に代入すると
$x^2+\cfrac{b}{a}x+\cfrac{c}{a}=0$
$ax^2+bx+c=0$
となります。これを逆向きにすると次のことが言えます。

これを解と係数の関係と言います。二次方程式の解が求められないとき，この関係を使って解を求められることがある，ということを覚えておきましょう。

実戦問題

$k$ を正の実数とし，2 次方程式 $8x^2-12kx+3k^2+8=0$ は $\sin\theta+2\cos\theta$，$2\sin\theta+\cos\theta$ を解に持つとする。ただし，$0\leqq\theta\leqq\cfrac{\pi}{4}$ とする。以下の問いに答えなさい。（東京都立大2017）
(1) $\sin\theta+\cos\theta$，$\sin\theta\cos\theta$ をそれぞれ $k$ を用いて表しなさい。
(2) $k$ の値を求めなさい。
(3) $\sin\theta$，$\cos\theta$ の値を求めなさい。

解と係数の関係を利用する

$8x^2-12kx+3k^2+8=0$ の解を
$\alpha=\sin\theta+2\cos\theta$
$\beta=2\sin\theta+\cos\theta$
とすると，解と係数の関係より
$\alpha+\beta=\cfrac{12k}{8}=\cfrac{3}{2}k$ ・・・①
$\alpha\beta=\cfrac{3k^2+8}{8}=\cfrac{3}{8}k^2+1$　・・・②
が成り立ちます。
①を変形して
$\sin\theta+2\cos\theta+2\sin\theta+\cos\theta=\cfrac{3}{2}k$
$3\sin\theta+3\cos\theta=\cfrac{3}{2}k$
$\sin\theta+\cos\theta=\cfrac{1}{2}k$
また
$\alpha\beta=(\sin\theta+2\cos\theta)(2\sin\theta+\cos\theta)$
$=2\sin^2\theta+5\sin\theta\cos\theta+2\cos^2\theta$
$=2(\sin^2\theta+\cos^2\theta)+5\sin\theta\cos\theta$
三角比の公式より $\sin^2\theta+\cos^2\theta=1$ だから
$=2+5\sin\theta\cos\theta$
②に代入して
$2+5\sin\theta\cos\theta=\cfrac{3}{8}k^2+1$
$\sin\theta\cos\theta=\cfrac{3}{40}k^2-\cfrac{1}{5}$
したがって
$\sin\theta+\cos\theta=\cfrac{1}{2}k$
$\sin\theta\cos\theta=\cfrac{3}{40}k^2-\cfrac{1}{5}$
（答え）

式を連立する

(2)に進みます。
(1)で求めた答えを連立して，$k$ の値を求めましょう。
$\sin\theta+\cos\theta=\cfrac{1}{2}k$　・・・③
$\sin\theta\cos\theta=\cfrac{3}{40}k^2-\cfrac{1}{5}$　・・・④
③を２乗すると④を利用できる形になりそうです。
$(\sin\theta+\cos\theta)^2=\cfrac{1}{4}k^2$
$\sin^2\theta+2\sin\theta\cos\theta+\cos^2\theta=\cfrac{1}{4}k^2$
$1+2\sin\theta\cos\theta=\cfrac{1}{4}k^2$
④を代入して
$1+2\Big(\cfrac{3}{40}k^2-\cfrac{1}{5}\Big)=\cfrac{1}{4}k^2$
$1+\cfrac{3}{20}k^2-\cfrac{2}{5}=\cfrac{1}{4}k^2$
分数のまま計算すると大変なので全体を20倍しておきましょう。
$20+3k^2-8=5k^2$
$2k^2=12$
$k^2=6$
$k=\pm\sqrt{6}$
問題文より，$k$ は正の実数だから
$k=\sqrt{6}$　（答え）

三角関数の合成

(3)に進みます。
三角関数の合成を使いましょう。
③より
$\sin\theta+\cos\theta=\cfrac{\sqrt{6}}{2}$
三角関数の合成を用いて
$\sqrt{2}\sin\Big(\theta+\cfrac{\pi}{4}\Big)=\cfrac{\sqrt{6}}{2}$

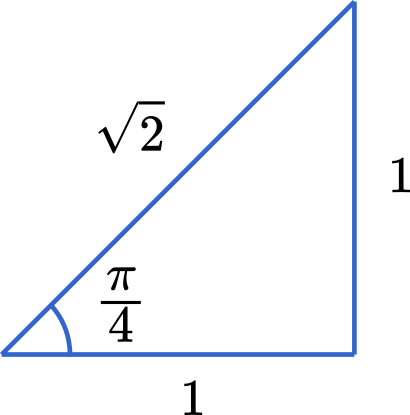
$\sin\Big(\theta+\cfrac{\pi}{4}\Big)=\cfrac{\sqrt{3}}{2}$
これに当てはまる $\theta+\cfrac{\pi}{4}$ の値は，$\cfrac{\pi}{3}$ と $\cfrac{2\pi}{3}$ の 2 個がありますが，
問題文より，$0\leqq\theta\leqq\cfrac{\pi}{4}$　だから
$\cfrac{\pi}{4}\leqq\theta+\cfrac{\pi}{4}\leqq\cfrac{\pi}{2}$ 
となるので，$\cfrac{\pi}{3}$ だけが当てはまります。
$\theta+\cfrac{\pi}{4}=\cfrac{\pi}{3}$
$\theta=\cfrac{\pi}{3}-\cfrac{\pi}{4}$
これを計算して $\cfrac{\pi}{3}-\cfrac{\pi}{4}=\cfrac{\pi}{12}$ とすると，$\sin\cfrac{\pi}{12}$ となり，値を求めることができません。
こういうときは，加法定理を使いましょう。
$\sin\Big(\cfrac{\pi}{3}-\cfrac{\pi}{4}\Big)=\sin\cfrac{\pi}{3}\cos\cfrac{\pi}{4}-\cos\cfrac{\pi}{3}\sin\cfrac{\pi}{4}$
$=\cfrac{\sqrt{3}}{2}\cdot\cfrac{\sqrt{2}}{2}-\cfrac{1}{2}\cdot\cfrac{\sqrt{2}}{2}$
$=\cfrac{\sqrt{6}-\sqrt{2}}{4}$
$\cos\Big(\cfrac{\pi}{3}-\cfrac{\pi}{4}\Big)=\cos\cfrac{\pi}{3}\cos\cfrac{\pi}{4}+\sin\cfrac{\pi}{3}\sin\cfrac{\pi}{4}$
$=\cfrac{1}{2}\cdot\cfrac{\sqrt{2}}{2}+\cfrac{\sqrt{3}}{2}\cdot\cfrac{\sqrt{2}}{2}$
$=\cfrac{\sqrt{2}+\sqrt{6}}{4}$
（答え）