【IA集合】部分集合に空集合が含まれるのはなぜ?をサイコロで考える(東京都立大2016文系第3問)





部分集合に空集合が含まれることを考慮する
ここで,特殊なサイコロを考えます。
このサイコロには 1 から 5 までの目は書いてありますが,普通なら 6 になる面には何も書かれていません。
そして集合を作ります。
$A=\{1,2,3\}$
$B=\{4,5\}$

このとき,サイコロの目が 1,2,3 のいずれかになる確率は
$\cfrac{1}{6}\times3=\cfrac{1}{2}$ ・・・①
次に,目が 4,5 のいずれかになる確率は
$\cfrac{1}{6}\times2=\cfrac{1}{3}$ ・・・②


全事象から①の $\cfrac{1}{2}$ を引いてみます。
$1-\cfrac{1}{2}=\cfrac{1}{2}$

なぜ,全事象から $A$ の確率を引いても $B$ の確率にならないのか。おおよそ見当はつくと思いますが,サイコロの何も書かれていない面が出る確率が抜けているからです。

そうとも言えますが,集合を書き直してみましょう。
$A=\{1,2,3\}$
$B=\{4,5\}$
$C=\phi$
空集合である集合 $C$ を加えてみました。サイコロの空白の面のことです。もちろん,サイコロを振ったとき $C$ になる確率は $\cfrac{1}{6}$ です。
余事象を求めてみましょう。
$P(B)=1-\{P(A)+P(C)\}$
$=1-\Big(\cfrac{1}{2}+\cfrac{1}{6}\Big)$
$=1-\cfrac{2}{3}$
$=\cfrac{1}{3}$

逆に $B$ の余事象から $A$ を求めてみます。
$P(A)=1-\{P(B)+P(C)\}$
$=1-\Big(\cfrac{1}{3}+\cfrac{1}{6}\Big)$
$=1-\cfrac{1}{2}$
$=\cfrac{1}{2}$
これも答えがちゃんと合っています。
こうして余事象を考えるとき,$A$ にも $B$ にも空集合が含まれていると考えなければつじつまが合いません。つまり,どんな部分集合にも空集合が含まれるということになります。

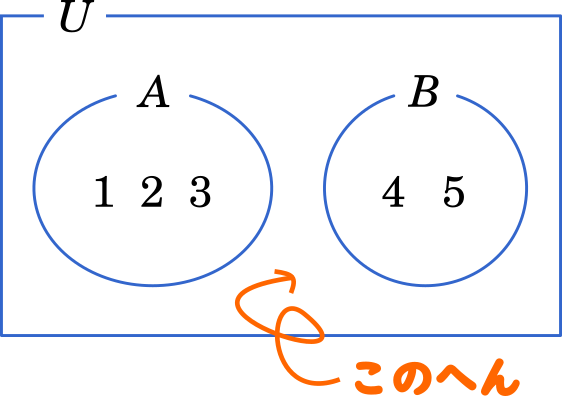


空集合の意味をもう少し掘り下げる
せっかく疑問を持ったので,もう少し話を掘り下げましょう。
例題で考えてみましょう。
全体集合 $U$ と部分集合 $A$,$B$ を以下のようにします。
$U=\{1,2,3,4,5,6\}$
$A=\{1,2,3\}$
$B=\{5,6\}$
$C=\phi$
今度はサイコロの目は 1,2,3,5,6 があり,残りの 1 つは空白です。つまり,4 がありません。
初めにサイコロをふるかふらないかを選択します。その確率はそれぞれ $\cfrac{1}{2}$ とします。
サイコロをふったとき,出た目を得点とします。一方で,サイコロをふらなかったとき,得点を 4 とします。

このとき,得点が 5 以上になる確率を余事象で求めてみましょう。



サイコロをふって 1,2,3 になる確率は $\cfrac{1}{2}\times\cfrac{1}{2}=\cfrac{1}{4}$ で,サイコロをふらない確率は $\cfrac{1}{2}$ だから
$1-\Big(\cfrac{1}{4}+\cfrac{1}{2}\Big)=1-\cfrac{3}{4}=\cfrac{1}{4}$



ここで上で出てきた疑問点,$\overline{A\cup B}$ と空集合はイコールではない,ということを確認しましょう。
サイコロをふって空白が出る確率は $\cfrac{1}{2}\times\cfrac{1}{6}=\cfrac{1}{12}$ だから
$P(B)=1-\{P(A)+P(C)+P(\overline{U})\}$
$=1-\Big(\cfrac{1}{4}+\cfrac{1}{12}+\cfrac{1}{2}\Big)$
$=1-\cfrac{10}{12}$
$=\cfrac{1}{6}$
こうして計算してみると,やはり $\overline{A\cup B}$ と空集合はイコールではないと考えないと,正しい答えを導くことはできません。ベン図で考えても,このことは空集合が $A$ の中に含まれると考えない限り説明がつきません。




今までサイコロの問題を解くときに,空集合のことを考えたことはないと思います。なぜなら,サイコロの目は必ず 1 から 6 のいずれかであり,サイコロの目が存在しない,というケースについては考えないからです。
しかし,厳密に言うと空集合が存在しないのではなく,存在していても空集合になる確率が 0 だから計算式に含めない,というが正しい解釈です。
こうなると,無いのにあるとか,あるのに無いとか,なんだか分からない世界に入り込んだような気持ちになるかもしれません。
普段は気にすることのない空集合ですが,空集合の確率が 0 でないときには,その確率を考慮するのを忘れないようにしましょう。存在しないと思っていたものも,こうしてときどきひょっこりと顔を出すものなのです。
演習問題
大小 2 つのサイコロを投げて出る目の値をそれぞれ $p,q$ とし,6 以下の自然数 $n$ のうち条件
$(n-p)(n-q)<0$
をみたすものすべてをホワイトボードに書くものとする。以下の問いに答えなさい。(東京都立大2016)
(1) ホワイトボードに 2 だけが書かれる確率を求めなさい。
(2) ホワイトボードに何も書かれない確率を求めなさい。
(3) ホワイトボードに書かれる自然数全体の集合を $A$ とする。ただし,何も書かれないとき $A$ は空集合とする。6 以下の素数全体の集合を $B$ とするとき,$A$ が $B$ の部分集合となる確率を求めなさい。
二次関数の解と確率
今回の問題のポイントは $p,q$ が二次関数の解を表していることです。ただし,解は $p<q$ のときと,$p>q$ のときがあるので注意しましょう。
$(n-p)(n-q)<0$
$p<q$ のとき,解は
$p<n<q$
また,$p>q$ のとき
$q<n<p$
$n=2$ とすると,$(p,q)=(1,3),(3,1)$
よって,確率は
$\cfrac{1}{6}\times\cfrac{1}{6}\times2=\cfrac{1}{18}$ (答え)
空集合になる確率
(2)に進みます。
$p<n<q$ に当てはまる $n$ が無いときを考えると,$p=q$ のときが考えれます。たとえば,$(p,q)=(3,3)$ なら $3<n<3$ となり,当てはまる自然数 $n$ は存在しません。このパターンは 6 通りあります。
あと一つ見逃しがちなのは,$(p,q)=(2,3)$ のようなケースです。これも,$2<n<3$ となり当てはまる $n$ は存在しません。このパターンは$(1,2)$ から $(5,6)$ までの 5 通りです。
$p=q$ のとき
$\cfrac{1}{6}\times\cfrac{1}{6}\times6=\cfrac{1}{6}$
$p,q$ が連続する 2 つの整数であるとき
$\cfrac{1}{6}\times\cfrac{1}{6}\times5\times2=\cfrac{5}{18}$
したがって
$\cfrac{1}{6}+\cfrac{5}{18}=\cfrac{4}{9}$ (答え)
空集合を含む確率
まず,集合 $B$ を求めましょう。$B$ は素数でした。
$B=\{2,3,5\}$
まず,$A$ が空集合のとき,(2)より確率は $\cfrac{4}{9}$ です。空集合も $B$ の部分集合に含まれることに注意してください。
よって
(i) $A=\{2\}$,$\{3\}$ ,$\{5\}$ のとき
(1)より当てはまる $n$ が 1 つだけのとき,確率は $\cfrac{1}{18}$ だから
$\cfrac{1}{18}\times3=\cfrac{1}{6}$
(ii) $A=\{2,3\}$ のとき
このとき,$(p,q)=(1,4),(4,1)$ だから
$\cfrac{1}{36}\times2=\cfrac{1}{18}$
(iii) $A=\phi$ のとき
(2)より $\cfrac{4}{9}$
したがって
$\cfrac{1}{6}+\cfrac{1}{18}+\cfrac{4}{9}=\cfrac{2}{3}$ (答え)
SNSでシェア