【数IIB微分積分】6分の1公式で突破！二次関数と直線で囲まれた面積の求め方・基本レベル(北海道大2021文系第4問)

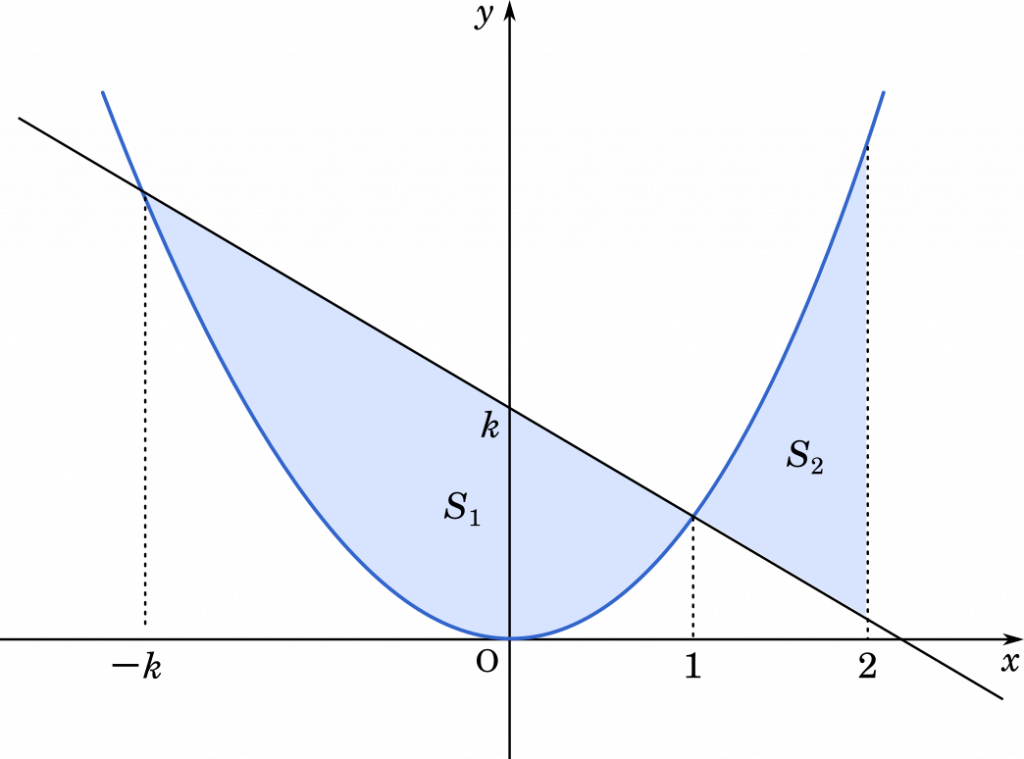
$k$ を $k>-1$ を満たす実数とする。直線 $\ell:y=(1-k)x+k$ および放物線 $C:y=x^2$ を考える。$C$ と $\ell$ で囲まれた部分の面積を $S_1$ とし，$C$ と $\ell$ と直線 $x=2$ の 3 つで囲まれた部分の面積を $S_2$ とする。（北海道大2021）

(1) $S_1$ を $k$ を用いて表せ。

(2) $S_2$ を $k$ を用いて表せ。

(3) $k$ が $k>-1$ を満たしながら動くとき，$S_2-S_1$ の最大値を求めよ。

初めに交点の座標を考える

(1)から始めます。

面積を求めるには，もう少し $S_1$ の形が分からないと話が進みません。そこで $\ell$ と $C$ の交点を求めることから始めましょう。

交点を求めるには，2 つの式を連立します。

$(1-k)x+k=x^2$
$x^2-(1-k)x-k=0$
$x=\cfrac{1-k\pm\sqrt{(1-k)^2+4k}}{2}$
$=\cfrac{1-k\pm\sqrt{1-2k+k^2+4k}}{2}$
$=\cfrac{1-k\pm\sqrt{1+2k+k^2}}{2}$
$=\cfrac{1-k\pm\sqrt{(1+k)^2}}{2}$

$k>-1$ より $1+k>0$ だから

$=\cfrac{(1-k)\pm(1+k)}{2}$
$=1,-k$

$x^2-(1-k)x-k=0$
$(x-1)(x+k)=0$
$x=1,-k$

6 分の 1 公式を使う

二次関数と直線において，2 つの交点の $x$ 座標が分かると，6 分の 1 公式が使えます。

したがって

$S_1=\cfrac{1}{6}(1+k)^3$　（答え）

積分で面積を求める

(2)に進みます。

今度は積分を使って面積を求めます。

$\displaystyle S_2=\int_1^2 x^2-(1-k)x-k\space dx$
$=\Big[\cfrac{x^3}{3}-\cfrac{1-k}{2}x^2-kx\Big]_1^2$
$=\cfrac{8}{3}-2(1-k)-2k-\Big(\cfrac{1}{3}-\cfrac{1-k}{2}-k\Big)$
$=\cfrac{8}{3}-2+2k-2k-\cfrac{1}{3}+\cfrac{1}{2}-\cfrac{k}{2}+k$

$=\cfrac{k}{2}+\cfrac{5}{6}$　（答え）

微分して増減表を作る

(3)に進みます。

$S_2-S_1=\cfrac{k}{2}+\cfrac{5}{6}-\cfrac{1}{6}(1+k)^3$
$=\cfrac{k}{2}+\cfrac{5}{6}-\cfrac{1}{6}(k^3+3k^2+3k+1)$
$=\cfrac{k}{2}+\cfrac{5}{6}-\cfrac{k^3}{6}-\cfrac{k^2}{2}-\cfrac{k}{2}-\cfrac{1}{6}$
$=-\cfrac{k^3}{6}-\cfrac{k^2}{2}+\cfrac{2}{3}$

$f(k)=-\cfrac{k^3}{6}-\cfrac{k^2}{2}+\cfrac{2}{3}$ として

$f'(k)=-\cfrac{k^2}{2}-k$

$-\cfrac{1}{2}k^2-k=0$ として

$\cfrac{k^2}{2}+k=0$
$k\Big(\cfrac{k}{2}+1\Big)=0$
$k=0,-2$

$k>-1$ より $k=0$

増減表は

$\def\arraystretch{1.5}\begin{array}{|c|c|c|c|c|}\hline k&(-1)&\cdots&0&\cdots \\\hline f'(k)&&+&0&-\\\hline f(k)&(\frac{1}{3})&\nearrow&\frac{2}{3}&\searrow\\\hline\end{array}$

$f\Big(\cfrac{1}{3}\Big)=-\cfrac{(-1)^3}{6}-\cfrac{(-1)^2}{2}+\cfrac{2}{3}$
$=\cfrac{1}{6}-\cfrac{1}{2}+\cfrac{2}{3}$
$=\cfrac{1-3+4}{6}=\cfrac{1}{3}$

$f(0)=\cfrac{2}{3}$

したがって，$S_2-S_1$ の最大値は $\cfrac{2}{3}$　（答え）