【数IIB点と直線の距離】正四面体でない四面体の内接球の半径を求める(九州大2021理系第1問)

座標空間内の 4 点 O$(0,0,0)$，A$(1,0,0)$，B$(0,1,0)$，C$(0,0,2)$ を考える。以下の問いに答えよ。（九州大2021）

(1) 四面体 OABC に内接する球の中心の座標を求めよ。

(2) 中心の $x$ 座標，$y$ 座標，$z$ 座標がすべて正の実数であり，$xy$ 平面，$yz$ 平面，$zx$ 平面のすべてと接する球を考える。この球が平面 ABC と交わるとき，その交わりとしてできる円の面積の最大値を求めよ。

新しい軸を作って考える

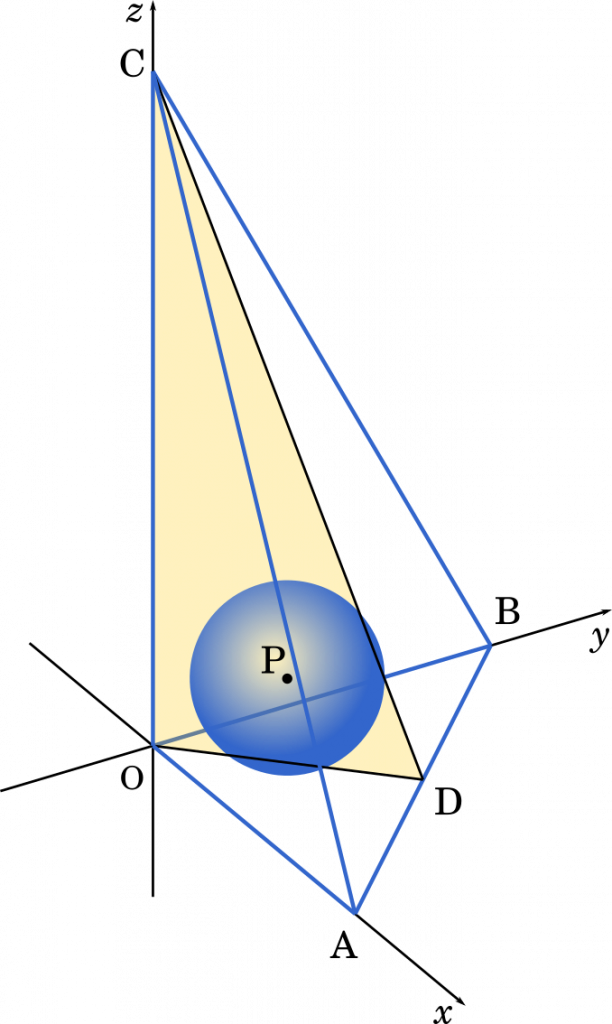
まず，四面体に内接する球であることから，球の中心 P は四面体の 4 つの三角形からの距離が等しい点となります。

考えてみると，△ABC からの距離は計算で出すのが難しそうですが，原点からの位置は $r$ を使って簡単に表すことができます。

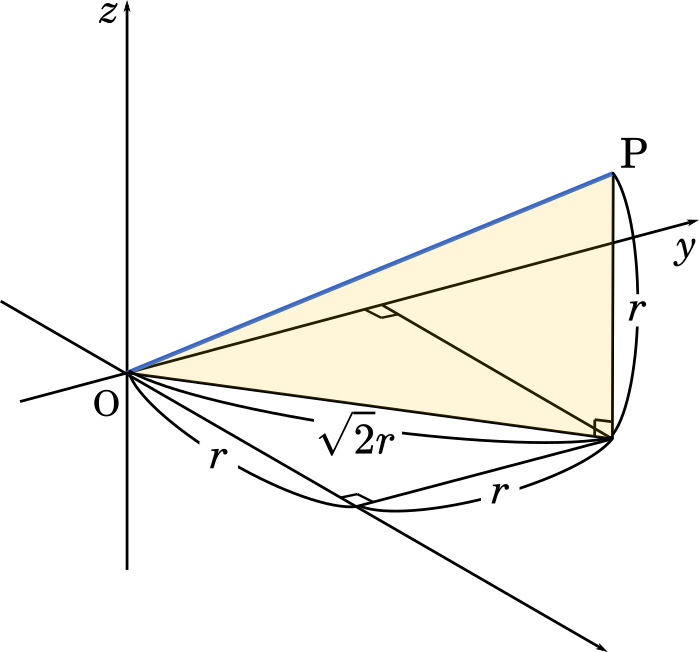
ここで AB の中点を D とすると球の中心 P は △OCD がつくる平面上にあることが分かります。また，△ABC と内接球の接点もこの平面に含まれます。

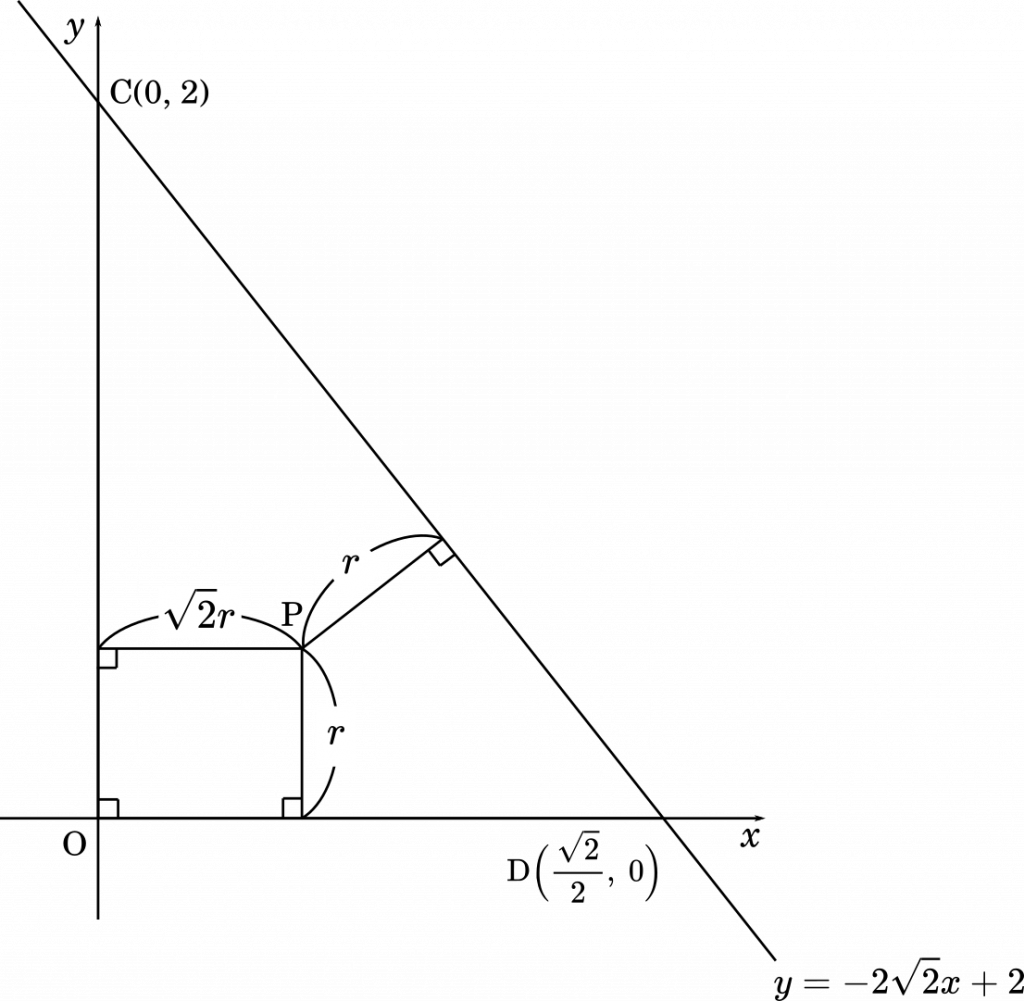
そこで，△OCD がつくる平面を軸として，新しい平面座標を作ってみます。
まず，線分 AB の中点 D の座標は

D ＝ $\cfrac{(1,0,0)+(0,1,0)}{2}$
$=\Big(\cfrac{1}{2},\space\cfrac{1}{2},\space0\Big)$

OD ＝ $\sqrt{\Big(\cfrac{1}{2}\Big)^2+\Big(\cfrac{1}{2}\Big)^2+0^2}$
$=\sqrt{\cfrac{1}{2}}=\cfrac{\sqrt{2}}{2}$

次に直線 CD の式を作りましょう。直線の傾きは

$\cfrac{0-2}{\cfrac{\sqrt{2}}{2}-0}=-\cfrac{2}{\cfrac{\sqrt{2}}{2}}$
$=-\cfrac{4}{\sqrt{2}}=-2\sqrt{2}$

よって直線の式は

$y=-2\sqrt{2}x+2$
$2\sqrt{2}x+y-2=0$

中心 P の座標を P$(\sqrt{2}r,\space r)$ とすると

点と直線の距離の公式より

$r=\cfrac{|2\sqrt{2}\cdot\sqrt{2}r+r-2|}{\sqrt{(2\sqrt{2})^2+1^2}}$
$=\cfrac{|5r-2|}{3}$

(i) $5r-2\geqq0$ のとき

$r=\cfrac{5r-2}{3}$
$3r=5r-2$
$-2r=-2$
$r=1$

このとき，点 P の座標は P$(1,1,1)$ となり，四面体の外側になるので，不適。

(ii) $5r-2<0$ のとき

$r=\cfrac{-5r+2}{3}$
$3r=-5r+2$
$8r=2$
$r=\cfrac{1}{4}$

したがって，球の座標は P$\Big(\cfrac{1}{4},\space\cfrac{1}{4},\space\cfrac{1}{4}\Big)$ （答え）

円を直線で切り取った辺の長さを考える

(2)に進みます。

立体で考えると平面 ABC と交わる円を考えるのはかなり想像力が必要ですが，(1)と同じように平面 OCD を軸とする平面で考えると，もう少しシンプルに捉えることができます。

(1)と同じように，球の座標は $\text{P}(\sqrt{2}r,r)$ として表すことができます。

このとき，△EHP に着目すると，EH が円の半径となり，これは三平方の定理を使って求めることができます。

$\text{P}(\sqrt{2}r,r)$ として，(1)より

$\text{PH}=\cfrac{|5r-2|}{3}$

三平方の定理より

$\text{EH}^2+\text{PH}^2=r^2$
$\text{EH}^2+\cfrac{(5r-2)^2}{9}=r^2$
$\text{EH}^2=r^2-\cfrac{(5r-2)^2}{9}$

$\text{EH}$ の最大値を求めます。そのために，$\text{EH}^2$ の最大値を求めます。

$\text{EH}^2=\cfrac{9r^2-25r^2+20r-4}{9}$
$=\cfrac{-16r^2+20r-4}{9}$

最大値を求めるために，平方完成しましょう。

$=-\cfrac{16}{9}\Big(r^2-\cfrac{9}{16}\cdot\cfrac{20}{9}r\Big)-\cfrac{4}{9}$
$=-\cfrac{16}{9}\Big(r^2-\cfrac{5}{4}r\Big)-\cfrac{4}{9}$
$=-\cfrac{16}{9}\Big(r-\cfrac{5}{8}\Big)^2+\cfrac{16}{9}\cdot\cfrac{25}{64}-\cfrac{4}{9}$
$=-\cfrac{16}{9}\Big(r-\cfrac{5}{8}\Big)^2+\cfrac{25}{36}-\cfrac{4}{9}$
$=-\cfrac{16}{9}\Big(r-\cfrac{5}{8}\Big)^2+\cfrac{1}{4}$

$\text{EH}^2$ の最大値は $\cfrac{1}{4}$
$\text{EH}$ の最大値は $\cfrac{1}{2}$

円の面積は

$\pi\Big(\cfrac{1}{2}\Big)^2=\cfrac{\pi}{4}$ （答え）