【数IIB確率分布と統計的な推測③】信頼度95%の信頼区間ってどういうこと？仕組みと求め方

読書アンケートで二項分布をざっくり理解してみる，二項分布を標準正規分布にするときの考え方で二項分布をもとに正規分布表を用いて確率を方法を学びました。今回は信頼区間について学んでいきましょう。

信頼区間 95 % の意味

ある学校で 100 人の生徒を選び，1 週間の読書時間を調査します。1 週間の読書時間の標本平均が 204 分，母標準偏差が 150 として，信頼度 95% の信頼区間を求めてみましょう。

そもそも信頼度 95% とはどういうことでしょうか。

ここでは標本平均を 204 分としていますが，それとは別に母平均というものが存在します。

母平均は学校の生徒全体の読書時間の平均です。生徒全体の平均と，そこから 100 人を選んだときの標本平均は同じでありません。

例えば，生徒全体の平均は 200 分なのに，選んだ生徒がたまたま読書しない生徒ばかりで，標本平均が 30 分だった，なんてことも起こり得ることです。

100 人を選んで調査した場合，母平均と標本平均が一致することはあり得ません。

そこで，標本平均に少し幅を持たせてみます。例えば，標本平均を 204 分とせずに，95% の信頼区間として 180 分から 230 分の間，$[180,230]$ と表してみます。

そして，再び 100 人を選んで同じ作業を何度も繰り返してみます。
そのときによって，区間は $[170,220]$，$[190,240]$，$[140,190]$・・・と様々な結果が出てきます。

このとき，読書時間の母平均が 200 分だったとして，調査の 95% ではその区間に 200 を含みます。逆に言えば，5% では $[140,190]$ ように，200 分を含まない範囲になることがあります。

ここで統計学を用いる意味が出てきます。母集団の数が多すぎて実際に調べることが難しいとき，一部を標本として調べ，統計学を用いてそこから母集団の平均を推定することができるのです。

信頼度 95% の信頼区間というのは，標本を選んで平均を出したときに，それを「だいたいここからここまでの間」というボンヤリした区間として表し，その調査を何度も行うと，調査の 95% では母平均がそれぞれの信頼区間に含まれているということです。

信頼区間の求め方

信頼度 95% の信頼区間を求めてみましょう。

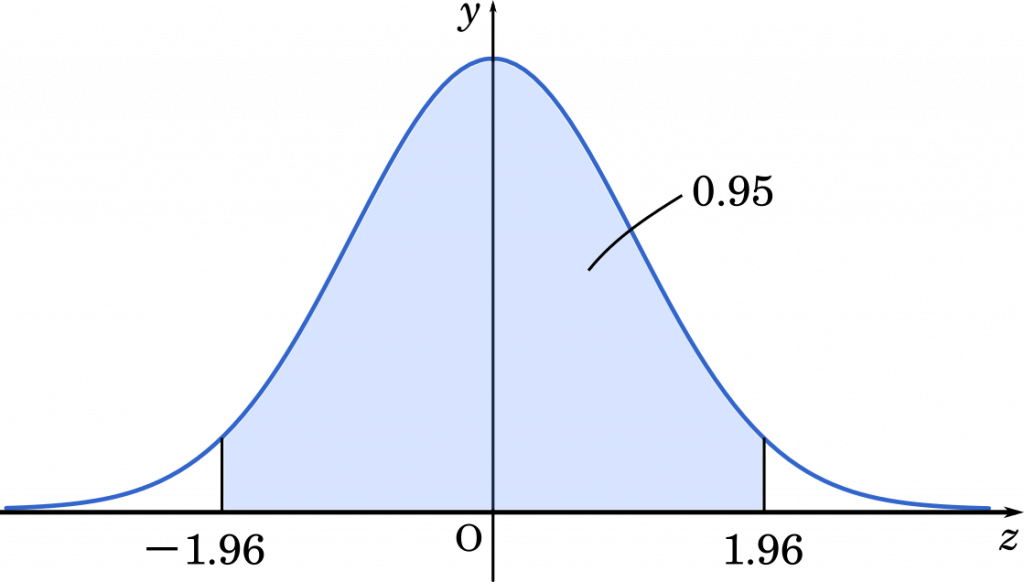
標準正規分布のグラフにおいて，グラフの塗りつぶした部分の面積が 95%，つまり 0.95 になるときの区間を考えます。

$0.95\div2=0.475$

グラフは $y$ 軸対称だから，片側の面積は 0.475 です。正規分布表で 0.475 を逆引きすると，確率変数の値は 1.96 です。従って，区間 $[-1.96,1.96]$ で確率が 0.95 になることが分かります。正規分布表は記事の最後に示しています。

1.96 という値はあくまで $N(0,1)$ の標準正規分布におけるグラフ上の話です。つまり，標本平均が 0 で，標準偏差が 1 の状態です。

先ほどの話に戻ると，正体の分からない母平均というものがもともと存在していて，調査を 100 回繰り返したら，95 回は $-1.96$ から $1.96$ の間に母平均が含まれていると推定できるということです。

ただし，正規分布を標準正規分布に変換しているので，もともとの母平均は $-1.96$ から $1.96$ の間の値ではないことに注意しましょう。

正規分布で考える場合，その区間はこのように表されます。

実際に計算してみる

標本の数が 100，1 週間の読書時間の標本平均が 204 分，母標準偏差が 150 として，信頼度 95% の信頼区間を求めてみましょう。

$n=100$，$\sigma=150$ として

$1.96\cdot\cfrac{\sigma}{\sqrt{n}}=1.96\times\cfrac{150}{\sqrt{100}}$
$=1.96\times\cfrac{150}{10}$
$=1.96\times15$
$=29.4$

よって，信頼区間は

$[204-29.4,204+29.4]$
$=[174.6,233.4]$

となります。

これで，学校全体の母平均は 174.6 分から 233.4 分の間にあることが推定できました。

まとめ

ここでは，抽出した標本から母平均を推定する方法を学びました。推定には母標準偏差の値が必要になりますが，実際には母集団の標準偏差は分からないことが多いので，代わりに標本の標準偏差を用いても構いません。ただし，標本の数が十分に大きいという条件があります。

正規分布表