【数IIB確率分布と統計的な推測①】読書アンケートで二項分布をざっくり理解してみる

無作為とは

学校で読書時間を調査したとします。全体の生徒数は分かりませんが，その中から 100 人を無作為に選びます。

母集団と標本

次に，全く読書をしなかった生徒の母比率を 0.5 とします。
母比率 0.5 は，たとえば，学校全体の生徒数を母集団として，それが 1,000 人いたとすると，その 50%（500人）が全く読書をしなかったということです。

100 人の選ばれた生徒のうち全く読書をしなかった生徒の比率を標本比率と言います。47 人が読書をしていなかったら，標本比率は 0.47 です。

このように，母比率と標本比率は同じ値になるとは限りません。

とは言え，母集団に対して抽出した標本の数が十分に大きければ，抽出したデータは母集団にかなり近いものになることが想像できます。

例えば，ペットを飼っている日本人の割合を調べたいとして，1 億人全員にアンケートを行うのは不可能です。そこで，その中から無作為に人を選んでアンケートを行えば，全体における割合を推定することができます。

二項分布

話を戻しましょう。学校全体から 100 人の生徒を選んで調査し，データを「読書をした」，「全く読書をしなかった」の 2 つに分けます。

全く読書をしなかった生徒の母比率が 0.5 なら，100 人のうち，全く読書をしなかった生徒の数は 50 人である可能性が最も高く，10 人や 90 人になる可能性はかなり低いことが想像できます。

これをグラフにしてみると，以下のようになります。

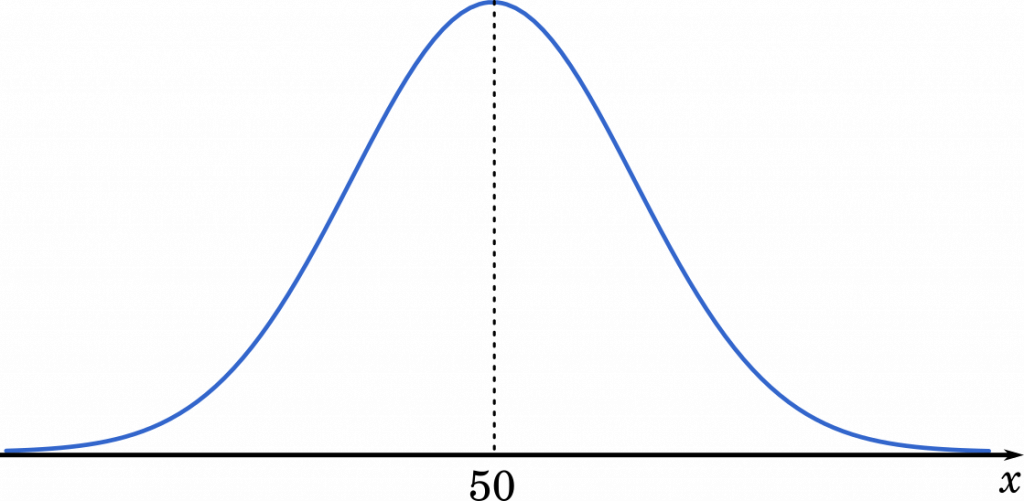
このようなグラフを正規分布曲線と言います。

このとき，グラフの横軸 $X$ を確率変数と言います。たとえば，$X=50$ のとき縦軸 $y$ は 0.1，$X=60$ のとき $y$ は 0.05 ・・・のように，$X$ に全く読書をしなかった生徒の数を代入すると，その確率が縦軸に表されます。

母比率が 0.5 だとしても，そこから無作為に抽出した標本で，全く読書をしなかった生徒が 50 人になるとは限りません。

全体の生徒から無作為に 100 人を選ぶという作業を何度も繰り返すことを想像しましょう。

選んだ生徒によって，全く読書をしなかった人数は 50 人だったり，60 人だったりします。作業を何度も繰り返すと，おそらく 50 人という結果が出る可能性が最も高く，60 人になる可能性はそれよりも低くなります。そうして得られた結果をグラフにしたものが上の正規分布曲線です。

二項分布の定義

今回のように，データを読書をした・しないで分けたとき，その確率分布を二項分布といい，確率変数 $X$ は二項分布 $B(100,0.5)$ に従うと言います。

一般的な形は，$B(n,p)$ で表され，$n$ は反復試行の回数，$p$ はある事象の起こる確率です。

100人を選んで全く読書をしなかった人数を調べる，という作業はこう言い換えることもできます。

生徒全体から無作為に 1 人の生徒を選び，読書の有無を調べる。このとき全く読書をしなかった確率は 0.5 である。これを 100 回繰り返す。

二項分布と正規分布

二項分布 $B(n,p)$ に従う確率変数 $X$ は，$n$ が十分大きいとき，正規分布に近似的に従います。

実際に問題を解くときには，二項分布を正規分布に変換して考えていきます。

結局のところ頭の中では二項分布は正規分布なのだと理解しておいて構いません。