【スマホで読む・わかりやすい】共通テスト数学IA2021第2日程【解説・正解・問題】

1 2 3 4 5

第1問　正解

アイ,ウエ　－2,－1　又は　－1,－2
オ　8　カ　3　キ　8　クケ　90
コ　4　サ　4　シ　1　ス　1　セ　0
ソ　0　タ　3　チ,ツ　4,5　テ　5

〔1〕(1)

∣ax−b−7∣<3|ax-b-7|<3 ・・・① として

a=−3,b=−2a=-3,b=-2 とすると，①は

∣−3x+2−7∣<3|-3x+2-7|<3
∣−3x−5∣<3|-3x-5|<3
−3<−3x−5<3-3<-3x-5<3
2<−3x<82<-3x<8
−83<x<−23-\cfrac{8}{3}<x<-\cfrac{2}{3}

これに当てはまる整数 xx は −1-1 と −2-2

よって P=−1,−2P={-1,-2}

・・・・・・アイ，ウエ

〔1〕(2)

a=12a=\cfrac{1}{\sqrt{2}} として

(i) b=1b=1 のとき①は

∣12x−1−7∣<3\Big|\cfrac{1}{\sqrt{2}}x-1-7\Big|<3
−3<12x−8<3-3<\cfrac{1}{\sqrt{2}}x-8<3
5<x2<115<\cfrac{x}{\sqrt{2}}<11

不等式に平方根があると範囲を求めることができないので，辺々を2乗して平方根を無くすことを考えると良い。

25<x22<12125<\cfrac{x^2}{2}<121
50<x2<24250<x^2<242

これに当てはまる xx を考えると，82=648^2=64，152=22515^2=225 だから，①を満たす整数は 8 から 15 までの 8 個である。

・・・オ

(ii)

①を満たす整数が 9 個のとき

∣12x−b−7∣<3\Big|\cfrac{1}{\sqrt{2}}x-b-7\Big|<3
−3<12−b−7<3-3<\cfrac{1}{\sqrt{2}}-b-7<3
4<12x−b<104<\cfrac{1}{\sqrt{2}}x-b<10
4+b<x2<10+b4+b<\cfrac{x}{\sqrt{2}}<10+b

辺々を 2 乗して

(4+b)2<x22<(10+b)2(4+b)^2<\cfrac{x^2}{2}<(10+b)^2
2(4+b)2<x2<2(10+b)22(4+b)^2<x^2<2(10+b)^2

b=2b=2 のとき

2×62<x2<2×1422\times6^2<x^2<2\times14^2
72<x2<28872<x^2<288

92=819^2=81，162=25616^2=256 より，①を満たす整数は 9 から 16 までの 8 個。よって，不適。

b=3b=3 のとき 

2×72<x2<2×1322\times7^2<x^2<2\times13^2
98<x2<33898<x^2<338

102=10010^2=100，182=32418^2=324 より，①を満たす整数は 10 から 18 までの 9 個。これは，問題文に適する。

したがって正の整数 bb のうち，最小のものは 3 である。

・・・カ

〔2〕(1)

正弦定理より

2R=ABsin⁡∠APB=8sin⁡∠APB2R=\cfrac{\text{AB}}{\sin\angle\text{APB}}=\cfrac{8}{\sin\angle\text{APB}}

・・・キ

R=4sin⁡∠APBR=\cfrac{4}{\sin\angle\text{APB}}

sin⁡\sin が最大のとき，RR は最小となる。sin⁡\sin は −1-1 から 11 までのいずれかの値をとるので，sin⁡∠APB=1\sin\angle\text{APB}=1 のとき ∠APB=90°\angle\text{APB}=90\degree であり

R=41=4R=\cfrac{4}{1}=4 

となる。

・・・クケ，コ

〔2〕(2)

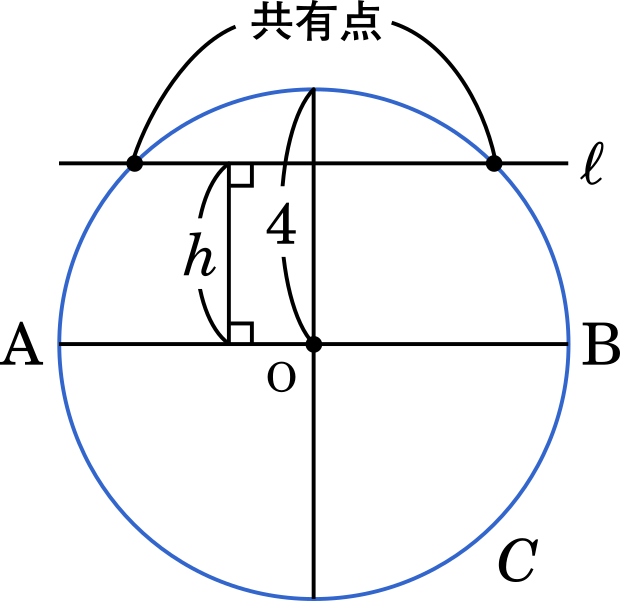
直線 ℓ\ell が円 CC と共有点を持つのは h≦4h\leqq4 のときである。

・・・サ

(i) h≦4h\leqq4 のとき

直線 AB は直径だから，△ABP は直角三角形である。

・・・シ

(ii) h>4h>4 のとき

円周角の定理より

∠AP3B=∠AP2B\angle\text{AP}_3\text{B}=\angle\text{AP}_2\text{B}

・・・ス

また，∠AP3B<∠AP1B<90°\angle\text{AP}_3\text{B}<\angle\text{AP}_1\text{B}<90\degree より

sin⁡∠AP3B<sin⁡∠AP1B\sin\angle\text{AP}_3\text{B}<\sin\angle\text{AP}_1\text{B}

つまり

sin⁡∠AP2B<sin⁡∠AP1B\sin\angle\text{AP}_2\text{B}<\sin\angle\text{AP}_1\text{B}

・・・セ

(1)で述べたように，sin⁡\sin の値が大きいほど，外接円の半径は小さくなるので

(△ABP1\text{ABP}_1の外接円の半径)＜(△ABP2\text{ABP}_2の外接円の半径)

である。

・・・ソ

これを基に考えると，直線 ℓ\ell 上の点のうち，外接円の半径が最も小さくなるのは，直線 mm との交点 P1\text{P}_1 のときである。

したがって，RR が最小となる△ABPは二等辺三角形である。

・・・タ

〔2〕(3)


sin⁡∠APB\sin\angle\text{APB} を求めるには，まず，AP，BP の長さを求め，余弦定理を用いて cos⁡∠APB\cos\angle\text{APB} を求める。cos⁡\cos の値が分かれば sin⁡\sin の値を求めることができる。

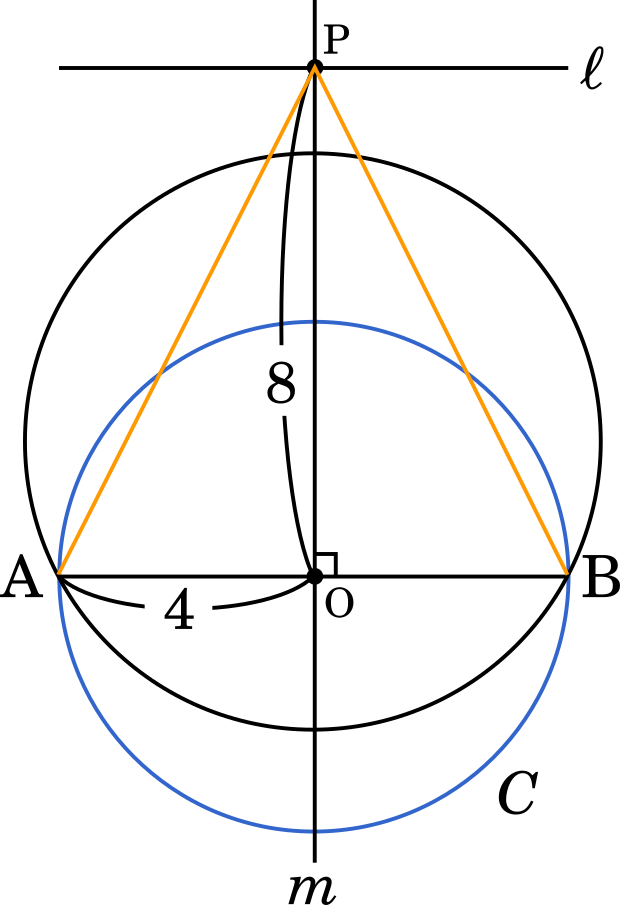
△AOP について，三平方の定理より

AP=42+82\text{AP}=\sqrt{4^2+8^2}
=80=45=\sqrt{80}=4\sqrt{5}

また，△ABPは二等辺三角形だから

 AP=BP=45\text{AP}=\text{BP}=4\sqrt{5}

余弦定理より

82=(45)2+(45)2−2⋅45⋅45cos⁡∠APB8^2=(4\sqrt{5})^2+(4\sqrt{5})^2-2\cdot4\sqrt{5}\cdot4\sqrt{5}\cos\angle\text{APB}
64=80+80−160cos⁡∠APB64=80+80-160\cos\angle\text{APB}
160cos⁡∠APB=96160\cos\angle\text{APB}=96
cos⁡∠APB=96160=35\cos\angle\text{APB}=\cfrac{96}{160}=\cfrac{3}{5}

公式 sin⁡2x+cos⁡2x=1\sin^2x+\cos^2x=1 より

sin⁡2∠APB+(35)2=1\sin^2\angle\text{APB}+\Big(\cfrac{3}{5}\Big)^2=1
sin⁡2∠APB=1−925=1625\sin^2\angle\text{APB}=1-\cfrac{9}{25}=\cfrac{16}{25}

0°<∠APB<90°0\degree<\angle\text{APB}<90\degree より，0<sin⁡∠APB<10<\sin\angle\text{APB}<1 だから

sin⁡∠APB=45\sin\angle\text{APB}=\cfrac{4}{5}

・・・チ，ツ

正弦定理より

2R= 8 45=8×545×52R=\cfrac{\space8\space}{\cfrac{4}{5}}=\cfrac{8\times5}{\cfrac{4}{5}\times5}
=404=10=\cfrac{40}{4}=10
R=5R=5

・・・テ

問題文

第1問 (必答問題)
〔1〕 aa，bb を定数とするとき，xx についての不等式

∣ax−b−7∣<3|ax-b-7|<3 ・・・・・・①

を考える。

(1) a=−3a=-3，b=−2b=-2 とする。①を満たす整数全体の集合を PP とする。この集合 PP を，要素を書き並べて表すと

P={アイ, ウエ}P=\{\boxed{\sf{アイ}},\space\boxed{\sf{ウエ}}\}

となる。ただし，アイ\boxed{\text{アイ}}，ウエ\boxed{\text{ウエ}} の解答の順序は問わない。

(2) a=12a=\cfrac{1}{\sqrt{2}} とする。

(i) b=1b=1 のとき，①を満たす整数は全部でオ\boxed{\sf{オ}}個である。

(ii) ①を満たす整数が全部で(オ+1)(\boxed{\text{オ}}+1)個であるような正の整数 bb のうち，最小のものはカ\boxed{\sf{カ}}である。

〔2〕 平面上に 2 点 A，B があり，AB = 8 である。直線 AB 上にない点 P をとり，△ABP をつくり，その外接円の半径を RR とする。

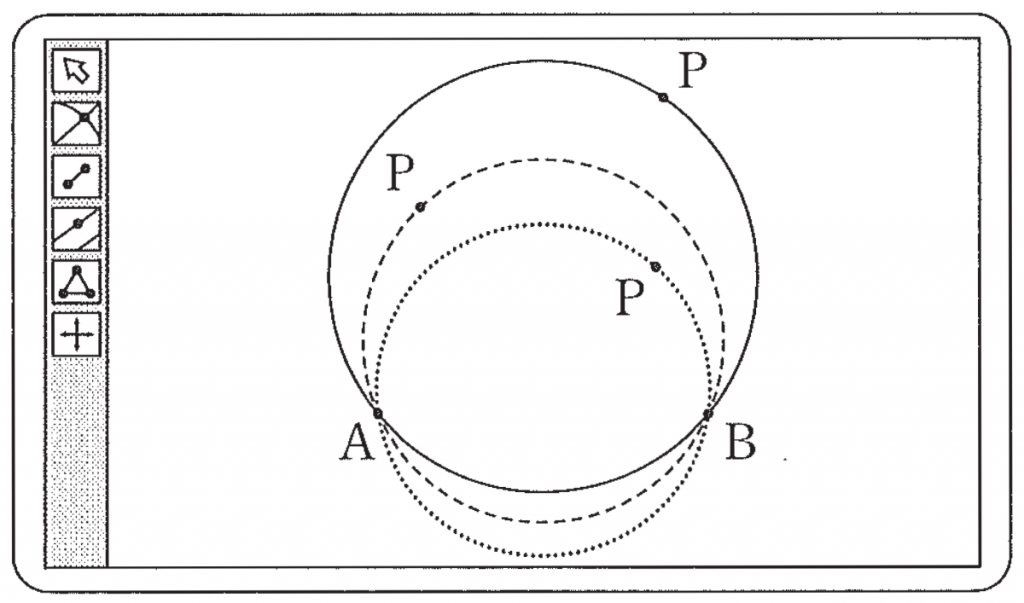
太郎さんは，図 1 のように，コンピュータソフトを使って点 P をいろいろな位置にとった。

図 1 は，点 P をいろいろな位置にとったときの △ABP の外接円をかいたものである。

図1

(1) 太郎さんは，点 P のとり方によって外接円の半径が異なることに気づき，次の問題1を考えることにした。

問題1 点 P をいろいろな位置にとるとき，外接円の半径 RR が最小となる △ABP はどのような三角形か。

正弦定理により，2R=キsin⁡∠APB2R=\cfrac{\boxed{\sf{キ}}}{\sin\angle\text{APB}} である。よって，RR が最小となるのは ∠APB=クケ°\angle\text{APB}=\boxed{\sf{クケ}}\degree の三角形である。このとき，R=コR=\boxed{\sf{コ}}である。

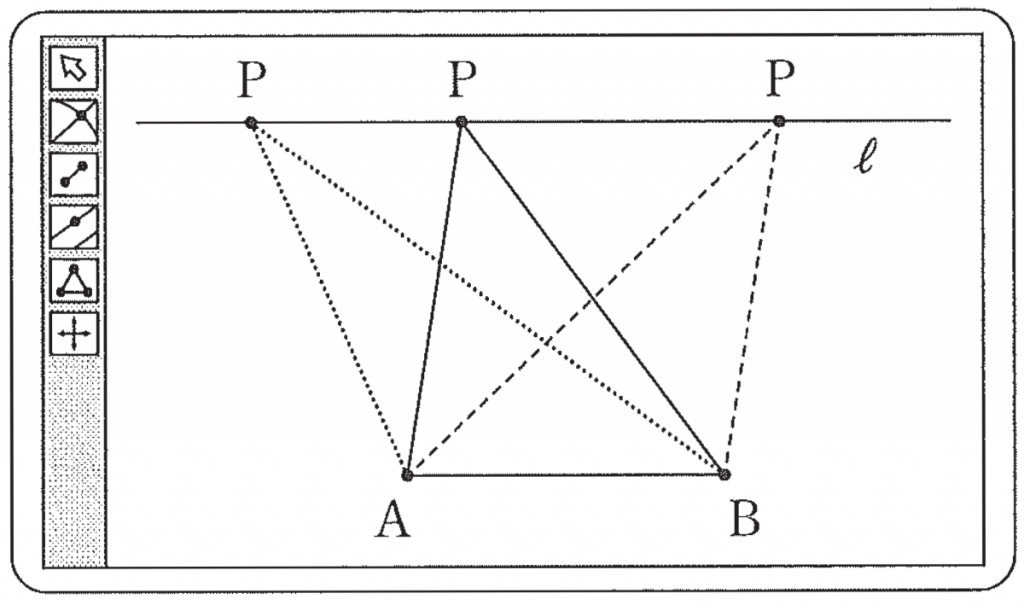
(2) 太郎さんは，図2のように，問題1の点 P のとり方に条件を付けて，次の問題2を考えた。

問題2　直線 AB に平行な直線を ℓ\ell とし，直線 ℓ\ell 上で点 P をいろいろな位置にとる。このとき，外接円の半径 RR が最小となる △ABP はどのような三角形か。

図2

太郎さんは，この問題を解決するために，次の構想を立てた。

問題2の解決の構想 

問題1の考察から，線分 AB を直径とする円を C とし，円 C に着目する。直線 ℓ\ell は，その位置によって，円 C と共有点をもつ場合ともたない場合があるので，それぞれの場合に分けて考える。

直線 AB と直線 ℓ\ell との距離を hh とする。直線 ℓ\ell が円 C と共有点をもつ場合は，h≦サh\leqq\boxed{\sf{サ}} のときであり，共有点をもたない場合は，h>サh>\boxed{\text{サ}} のときである。

(i) h≦サh\leqq\boxed{\text{サ}} のとき

直線 ℓ\ell が円 C と共有点をもつので，RR が最小となる △ABP は，h<サh<\boxed{\text{サ}} のとき シ\boxed{\boxed{\sf{シ}}} であり，h=サh=\boxed{\text{サ}} のとき直角二等辺三角形である。

(ii) h>サh>\boxed{\text{サ}} のとき

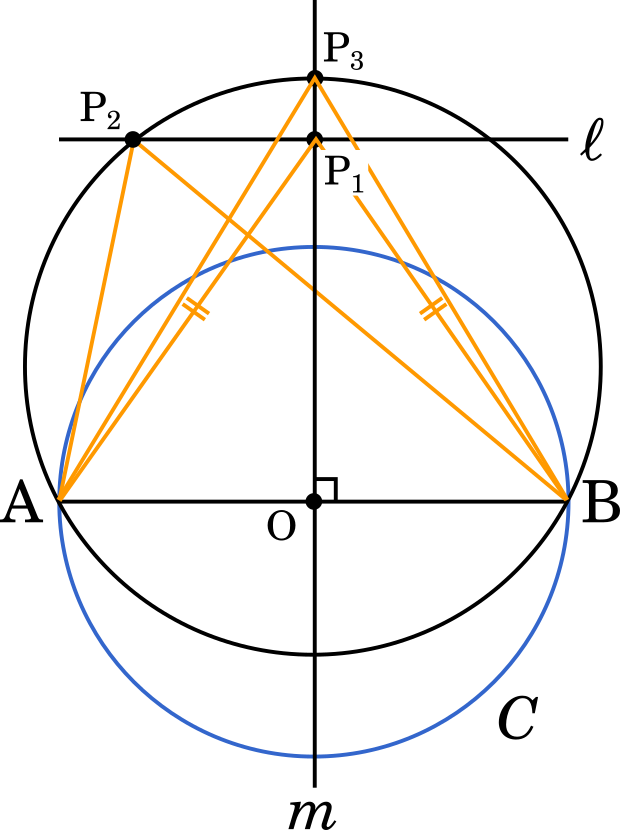
線分 AB の垂直二等分線を mm とし，直線 mm と直線 ℓ\ell との交点を P1\text{P}_1 とする。直線 ℓ\ell 上にあり点 P1\text{P}_1 とは異なる点を P2\text{P}_2 とするとき sin⁡∠AP1B\sin\angle\text{AP}_1\text{B} と sin⁡∠AP2B\sin\angle\text{AP}_2\text{B} の大小を考える。

△ABP2\text{ABP}_2 の外接円と直線 mm との共有点のうち，直線 AB に関して点 P2\text{P}_2 と同じ側にある点を P3\text{P}_3 とすると，∠AP3Bセsin⁡∠AP1B\angle\text{AP}_3\text{B}\boxed{\boxed{\sf{セ}}}\sin\angle\text{AP}_1\text{B} である。このとき

(△ABP1\text{ABP}_1 の外接円の半径) ソ\boxed{\boxed{\sf{ソ}}} (△ABP2\text{ABP}_2 の外接円の半径)
であり，RR が最小となる △ABP は タ\boxed{\boxed{\sf{タ}}} である。

シ\boxed{\boxed{\text{シ}}}，タ\boxed{\boxed{\text{タ}}} については，最も適当なものを，次の⓪～④のうちから一つずつ選べ。ただし，同じものを繰り返し選んでもよい。

⓪ 鈍角三角形　① 直角三角形
② 正三角形　③ 二等辺三角形
④ 直角二等辺三角形 

ス\boxed{\boxed{\text{ス}}}～ソ\boxed{\boxed{\text{ソ}}} の解答群(同じものを繰り返し選んでもよい。) 

⓪ <<　① ==　② >>

(3) 問題2の考察を振り返って，h=8h=8 のとき，△ABP の外接円の半径 RR が最小である場合について考える。このとき，sin⁡∠APB=チツ\sin\angle\text{APB}=\cfrac{\boxed{\sf{チ}}}{\boxed{\sf{ツ}}} であり，R=テR=\boxed{\sf{テ}} である。

1 2 3 4 5

SNSでシェア

mm参考書 2019-2023