【スマホで読む・わかりやすい】共通テスト数学IIB2021本試【解説・正解・問題】
第1問 正解
ア 3 イ 2 ウ 6 エ 2
オ 2 カ 1 キ 9 ク 1
ケ 3 コ,サ 1,9 シ,ス 2,1
セ 1 ソ 0 タ 0 チ 1
ツ,テ 5,2 ト 0 ナ 3 ニ 1
ヌ 2 ネ 1
〔1〕(1)
$y=\sin\theta+\sqrt{3}\cos\theta\Big(0\leqq\theta\leqq\cfrac{\pi}{2}\Big)$
より,三角関数の合成を用いて
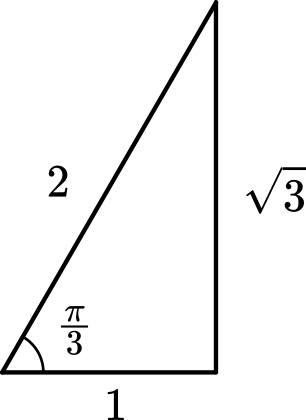
$\sin\cfrac{\pi}{3}=\cfrac{\sqrt{3}}{2}$,$\cos\cfrac{\pi}{3}=\cfrac{1}{2}$
・・・ア
また
$y=2\sin\Big(\theta+\cfrac{\pi}{3}\Big)$
・・・イ
$\sin$ の値は $-1$ から $1$ の間のいずれかであることから ,最大値は $\sin\Big(\theta+\cfrac{\pi}{3}\Big)=1$ のときである。よって
$\theta+\cfrac{\pi}{3}=\cfrac{\pi}{2}$
$\theta=\cfrac{\pi}{2}-\cfrac{\pi}{3}=\cfrac{\pi}{6}$
・・・ウ
$\theta=\cfrac{\pi}{6}$ として,最大値は
$y=2\sin\Big(\theta+\cfrac{\pi}{3}\Big)=2\cdot1=2$
・・・エ
〔1〕(2)
$y=\sin\theta+p\cos\theta\Big(0\leqq\theta\leqq\cfrac{\pi}{2}\Big)$
として
(i) $p=0$ のとき
$y=\sin\theta$
したがって,$y$ は $\theta=\cfrac{\pi}{2}$ で最大値 $1$ をとる。
・・・・・・オカ
(ii) $p>0$ のとき
ここでは,三角関数の合成が成り立つ仕組みを理解しているかどうかが問われている。それを証明するためには,逆向きに考えていくと良い。
$r\sin(\theta+\alpha)=r\sin\theta\cos\alpha+r\cos\theta\sin\alpha$
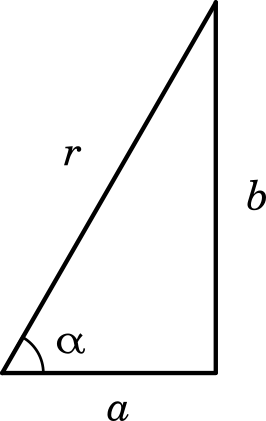
ここで,$r\cos\alpha=a$,$r\sin\alpha=b$ とすると
$a\sin\theta+b\cos\theta=r\sin(\theta+\alpha)$ (証明終わり)
これと同じ考え方を $\cos$ の加法定理に当てはめていく。
$\cos(\theta-\alpha)=\cos\theta\cos\alpha+\sin\theta\sin\alpha$
両辺に $r$ をかけて
$r\cos(\theta-\alpha)=r\cos\theta\cos\alpha+r\sin\theta\sin\alpha$
次に,問題文の式 $\sin\theta+p\cos\theta$ にあわせるために,$r\cos\alpha=p$,$r\sin\alpha=1$ となる三角形を作ると良い。
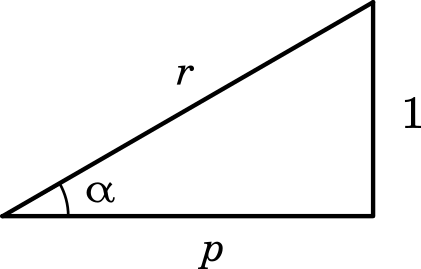
$r\cos\alpha=p$,$r\sin\alpha=1$ とすると
$r\cos(\theta-\alpha)=\sin\theta+p\cos\theta$
となる。
$r$ を求めると,上の図より三平方の定理を用いて
$r=\sqrt{1+p^2}$
したがって
$y=\sin\theta+p\cos\theta=\sqrt{1+p^2}\cos(\theta-\alpha)$
・・・キ
また,$\sin\alpha=\cfrac{1}{r}$,$\cos\alpha=\cfrac{p}{r}$ より
$\sin\alpha=\cfrac{1}{\sqrt{1+p^2}}$,$\cos\alpha=\cfrac{p}{\sqrt{1+p^2}}$
・・・クケ
最大値を求めると,$\cos$ の値は $-1$ から $1$ のいずれかだから,最大値は
$\cos(\theta-\alpha)=1$
のときである。
したがって
$\theta-\alpha=0$
$\theta=\alpha$
・・・コ
このとき $y$ は
$\theta-\alpha=0$ を $y=\sqrt{1+p^2}\cos(\theta-\alpha)$ に代入して
$y=\sqrt{1+p^2}$
・・・サ
(iii)
$p<0$ のとき
$p$ のままでは分かりにくいので,仮に $p=-2$ として考えてみる。このとき
$y=\sin\theta+p\cos\theta=\sin\theta-2\cos\theta$
となる。$0\leqq\theta\leqq\cfrac{\pi}{2}$ より,$\theta$ を $0$ から $\cfrac{\pi}{2}$ まで変化させると $\sin\theta$ は $0$ から $1$ まで増加する。また,$\cos\theta$ は $1$ から $0$ まで変化するので,$-2\cos\theta$ は $-2$ から $0$ まで増加する。
したがって,$y$ は $\theta=\cfrac{\pi}{2}$ で最大となり,最大値は
$y=\sin\cfrac{\pi}{2}+p\cos\cfrac{\pi}{2}=1$
・・・シ,ス
〔2〕(1)
$f(x)=\cfrac{2^x+2^{-x}}{2}$,$g(x)=\cfrac{2^x-2^{-x}}{2}$
として
$f(0)=\cfrac{2^0+2^{-0}}{2}$
$=\cfrac{1+1}{2}=1$
・・・セ
$g(0)=\cfrac{2^0-2^{-0}}{2}$
$=\cfrac{1-1}{2}=0$
・・・ソ
$f(x)=\cfrac{2^x}{2}+\cfrac{2^{-x}}{2}$ として
相加・相乗平均の関係 $a+b\geqq2\sqrt{ab}$ より
$\begin{aligned}\cfrac{2^x}{2}+\cfrac{2^{-x}}{2}&\geqq2\sqrt{\cfrac{2^x}{2}\cdot\cfrac{2^{-x}}{2}}\\&\geqq2\sqrt{\cfrac{2^0}{4}}\\&\geqq2\cdot\cfrac{1}{2}\\&\geqq1\end{aligned}$
よって,$f(x)$ の最小値は $1$ である。このとき,上で求めた通り,$f(0)=1$ だから
$f(x)$ は $x=0$ で最小値 $1$ をとる。
・・・タ,チ
次に,$g(x)=-2$ とする。
$g(x)=\cfrac{2^x-2^{-x}}{2}=-2$
問題文より $\log$ を用いることを念頭に置いて,式を変形していくと良い。
$2^x-2^{-x}=-4$
$2^x-\cfrac{1}{2^x}=-4$
ここで,$2^x=t$ とおくと
$t-\cfrac{1}{t}=-4$
両辺を $t$ 倍して
$t^2-1=-4t$
$t^2+4t-1=0$
$t=-2\pm\sqrt{1+4}$
$t=-2\pm\sqrt{5}$
ここで,$2^x$ は $x$ にどのような値を代入しても正の数となることに注意して
$t>0$ より
$t=-2+\sqrt{5}$
$2^x=\sqrt{5}-2$
底を $2$ として両辺の対数をとると
$\log_22^x=\log_2(\sqrt{5}-2)$
$x\log_22=\log_2(\sqrt{5}-2)$
$x\cdot1=\log_2(\sqrt{5}-2)$
$x=\log_2(\sqrt{5}-2)$
・・・ツ,テ
〔2〕(2)
実際に値を代入して計算してみると良い。
①は
$f(-x)=\cfrac{2^{-x}+2^x}{2}=f(x)$
・・・ト
②は
$g(-x)=\cfrac{2^{-x}-2^x}{2}$
$=-\cfrac{2^x-2^{-x}}{2}=-g(x)$
・・・ナ
③は
$\{f(x)\}^2-\{g(x)\}^2$
因数分解して
$=\{f(x)+g(x)\}\{f(x)-g(x)\}$
ここで
$f(x)+g(x)=\cfrac{2^x+2^{-x}}{2}+\cfrac{2^x-2^{-x}}{2}$
$=2^x$
$f(x)-g(x)=\cfrac{2^x+2^{-x}}{2}-\cfrac{2^x-2^{-x}}{2}$
$=2^{-x}$
だから
$\{f(x)+g(x)\}\{f(x)-g(x)\}=2^x\cdot2^{-x}$
$=2^0=1$
・・・ニ
④は
左辺について
$g(2x)=\cfrac{2^{2x}-2^{-2x}}{2}$
また,右辺は
$f(x)g(x)=\cfrac{2^x+2^{-x}}{2}\cdot \cfrac{2^x-2^{-x}}{2}$
$=\cfrac{(2^x+2^{-x})(2^x-2^{-x})}{4}$
$=\cfrac{2^{2x}-2^{-2x}}{4}$
だから
$g(2x)=2f(x)g(x)$
・・・ヌ
〔2〕(3)
問題文の花子の発言をもとに,$\beta$ に具体的な値,つまり $\beta=0$ を代入してみると,(1)で求めた $f(0)=1$,$g(0)=0$ が利用できる。
(A)は
$f(\alpha-0)=f(\alpha)g(0)+g(\alpha)f(0)$
$f(\alpha)=f(\alpha)\cdot0+g(\alpha)\cdot1$
$=g(\alpha)$
左辺と右辺が一致しないので,不適。
(B)は
$f(\alpha+0)=f(\alpha)f(0)+g(\alpha)g(0)$
$f(\alpha)=f(\alpha)\cdot 1+g(\alpha)\cdot0$
$=f(\alpha)$
左辺と右辺が一致するので,式は成り立つ。
(C)は
$g(\alpha-0)=f(\alpha)f(0)+g(\alpha)g(0)$
$g(\alpha)=f(\alpha)\cdot1+g(\alpha)\cdot0$
$=f(\alpha)$
左辺と右辺が一致しないので,不適。
(D)は
$g(\alpha+0)=f(\alpha)g(0)-g(\alpha)f(0)$
$g(\alpha)=f(\alpha)\cdot0-g(\alpha)\cdot1$
$=-g(\alpha)$
左辺と右辺が一致しないので,不適。
従って,(B) 以外の三つは成り立たないことがわかる。
・・・ネ
解答としてはこれで良いが,(B)が実際に成り立つかどうかを確認しておこう。
(B)の左辺について
$f(\alpha+\beta)=\cfrac{2^{\alpha+\beta}+2^{-(\alpha+\beta)}}{2}$
右辺について
$f(\alpha)f(\beta)+g(\alpha)g(\beta)$
$=\cfrac{2^\alpha+2^{-\alpha}}{2}\cdot\cfrac{2^\beta+2^{-\beta}}{2}+\cfrac{2^\alpha-2^{-\alpha}}{2}\cdot\cfrac{2^\beta-2^{-\beta}}{2}$
$=\cfrac{1}{4}\{2^{\alpha+\beta}+2^{\alpha-\beta}+2^{\beta-\alpha}+2^{-(\alpha+\beta)}+2^{\alpha+\beta}-2^{\alpha-\beta}-2^{\beta-\alpha}+2^{-(\alpha+\beta)}\}$
$=\cfrac{2^{\alpha+\beta}+2^{-(\alpha+\beta)}}{2}$
左辺と右辺が一致するので,式は成り立つ。
問題文
第1問
〔1〕
(1) 次の問題 Aについて考えよう。
問題A 関数 $y=\sin\theta+\sqrt{3}\cos\theta$ $\Big(0\leqq\theta\leqq\cfrac{\pi}{2}\Big)$ の最大値を求めよ。
$\sin\cfrac{\pi}{\boxed{\sf ア}}=\cfrac{\sqrt{3}}{2}$,$\cos\cfrac{\pi}{\boxed{\text ア}}=\cfrac{1}{2}$
であるから,三角関数の合成により
$y=\boxed{\sf イ}\sin\Big(\theta+\cfrac{\pi}{\boxed{\text ア}}\Big)$
と変形できる。よって,$y$ は $\theta=\cfrac{\pi}{\boxed{\sf ウ}}$ で最大値 $\boxed{\sf エ}$ をとる。
(2) $p$ を定数とし,次の問題Bについて考えよう。
問題B 関数 $y=\sin\theta+p\cos\theta$ $\Big(0\leqq\theta\leqq\cfrac{\pi}{2}\Big)$ の最大値を求めよ。
(i) $p=0$ のとき,$y$ は $\theta=\cfrac{\pi}{\boxed{\sf オ}}$ で最大値 $\boxed{\sf カ}$ をとる。
(ii) $p>0$ のときは,加法定理
$\cos(\theta-\alpha)=\cos\theta\cos\alpha+\sin\theta\sin\alpha$
を用いると
$y=\sin\theta+p\cos\theta=\sqrt{\boxed{\boxed{\sf キ}}}\cos(\theta-\alpha)$
と表すことができる。ただし,$\alpha$ は
$\sin\alpha=\cfrac{\boxed{\boxed{\sf ク}}}{\sqrt{\boxed{\text キ}}}$,$\cos\alpha=\cfrac{\boxed{\boxed{\sf ケ}}}{\sqrt{\boxed{\text キ}}}$,$0<\alpha<\cfrac{\pi}{2}$
を満たすものとする。このとき,$y$ は $\theta=\boxed{\boxed{\text コ}}$
で最大値 $\sqrt{\boxed{\boxed{\sf サ}}}$ をとる。
(iii) $p<0$ のとき,$y$ は $\theta=\boxed{\boxed{シ}}$ で最大値 $\theta=\boxed{\boxed{ス}}$ をとる。
$\boxed{\boxed{キ}}$ ~ $\boxed{\boxed{ケ}}$,$\boxed{\boxed{サ}}$,$\boxed{\boxed{ス}}$ の解答群(同じものを繰り返し選んでもよい。)
⓪ $-1$ ① $1$ ② $-p$
③ $p$ ④ $1-p$ ⑤ $1+p$
⑥ $-p^2$ ⑦ $p^2$ ⑧ $1-p^2$
⑨ $1+p^2$ $\text{\textcircled a}$ $(1-p)^2$ $\text{\textcircled b}$ $(1+p)^2$
$\boxed{\boxed{コ}}$,$\boxed{\boxed{シ}}$ の解答群 (同じものを繰り返し選んでもよい。)
⓪ $0$ ① $\alpha$ ② $\cfrac{\pi}{2}$
〔2〕 二つの関数 $f(x)=\cfrac{2^x+2^{-x}}{2}$,$g(x)=\cfrac{2^x-2^{-x}}{2}$ について考える。
(1) $f(0)=\boxed{\sf セ}$,$g(0)=\boxed{\sf ソ}$ である。また,$f(x)$ は相加平均と相乗平均の関係から,$x=\boxed{\sf タ}$ で最小値 $\boxed{\sf テ}$ をとる。$g(x)=-2$ となる $x$ の値は $\log_2(\sqrt{\boxed{\sf ツ}}-\boxed{\sf テ})$ である。
(2) 次の①~④は,$x$ にどのような値を代入してもつねに成り立つ。
$f(-x)=\boxed{\boxed{\sf ト}}$ ・・・・・・①
$g(-x)=\boxed{\boxed{\sf ナ}}$ ・・・・・・②
$\{f(x)\}^2-\{g(x)\}^2=\boxed{\sf ニ}$ ・・・・・・③
$g(2x)=\boxed{\sf ヌ}f(x)g(x)$ ・・・・・・④
$\boxed{\boxed{\text ト}}$,$\boxed{\boxed{\text ナ}}$ の解答群(同じものを繰り返し選んでもよい。)
⓪ $f(x)$ ① $-f(x)$ ② $g(x)$ ③ $-g(x)$
(3) 花子さんと太郎さんは,$f(x)$ と $g(x)$ の性質について話している。
花子:①~④は三角関数の性質に似ているね。
太郎:三角関数の加法定理に類似した式(A)~(D)を考えてみたけど,つねに成り立つ式はあるだろうか。
花子:成り立たない式を見つけるために,式(A)~(D)の $\beta$ に何か具体的な値を代入して調べてみたらどうかな。
太郎さんが考えた式
$f(\alpha-\beta)=f(\alpha)g(\beta)+g(\alpha)f(\beta)$ ・・・・・・(A)
$f(\alpha+\beta)=f(\alpha)f(\beta)+g(\alpha)g(\beta)$ ・・・・・・(B)
$g(\alpha-\beta)=f(\alpha)f(\beta)+g(\alpha)g(\beta)$ ・・・・・・(C)
$g(\alpha+\beta)=f(\alpha)g(\beta)-g(\alpha)f(\beta)$ ・・・・・・(D)
(1),(2)で示されたことのいくつかを利用すると,式(A)~(D)のうち,$\boxed{\boxed{\sf ネ}}$ 以外の三つは成り立たないことがわかる。$\boxed{\boxed{\text ネ}}$ は左辺と右辺をそれぞれ計算することによって成り立つことが確かめられる。
$\boxed{\boxed{\text ネ}}$ の解答群
⓪ (A) ① (B) ② (C) ③ (D)
SNSでシェア