【数II高次方程式】因数定理と組立除法でなぜ因数分解できるのか納得いかない

剰余の定理

たとえば，次のような式を考えます。

$P(x)=x^2-x-2+3$
$=(x+1)(x-2)+3$

この式を割る数×商＋余りとして見なすと，整式 $P(x)$ を $x+1$ で割った商は $x-2$ で余りは $3$ と言うことができます。

ここで，$x$ に $-1$ を代入してみます。

$P(-1)=(-1+1)(-1-2)+3$
$=0+3$ 

つまり

$P(-1)=3$

こうして，式を $x+1$ で割るとき，$x=-1$ を代入するだけで，余りを求めることができます。この考え方を剰余の定理と言います。

余りが 0 になる場合

次に，このような式を考えます。

$P(x)=x^2-x-2$
$=(x+1)(x-2)+0$

同じように式を割る数×商＋余りとして見なすと，整式 $P(x)$ を $x+1$ で割った商は $x-2$ で余りは $0$ と言うことができます。

剰余の定理から言えば，$x+1$ で割った余りは $P(-1)$ で求めることができます。今回は余りが $0$ だから

$P(-1)=0$

ということになります。

$P(-1)=(-1+1)(-1-2)+0=0$

$x^2-x-2$ が $(x+1)(x-2)$ になるということは，言い換えれば因数分解できるということです。

因数定理

この考えを因数定理としてまとめます。

$P(x)=x^2-x-2$ は $x+1$ と $x-2$ を因数に持ちます。このとき

$P(-1)=(-1)^2-(-1)-2=0$
$P(2)=2^2-2-2=0$

確かに余りが 0 になることが確かめられました。

ここから，次のことが言えます。

たとえば，ある整式 $P(x)$ が $P(1)=0$ となるなら，式は $x-1$ を因数として因数分解でき，また $P(-2)=0$ となるなら式は $x+2$ で因数分解できる。

この考えは，式の因数分解に使えそうです。練習問題で確かめてみましょう。

練習問題

[問題] $x^3-4x^2+x+6$ を因数分解せよ。

まず，$x$ に数を代入して $=0$ となる数を見つけます。

一般的には $1,-1,2,-2,\cdots$ の順に代入していくと良いでしょう。

そうすると，$x=-1$ のとき，式が $=0$ になります。

$P(x)=x^3-4x^2+x+6$ として
$P(-1)=(-1)^3-4(-1)^2+(-1)+6=0$

よって，式は $x+1$ で割り切れることが分かります。

実際に割ってみましょう。

組立除法

式を $x+1$ のような形で割るときには組立除法を用います。

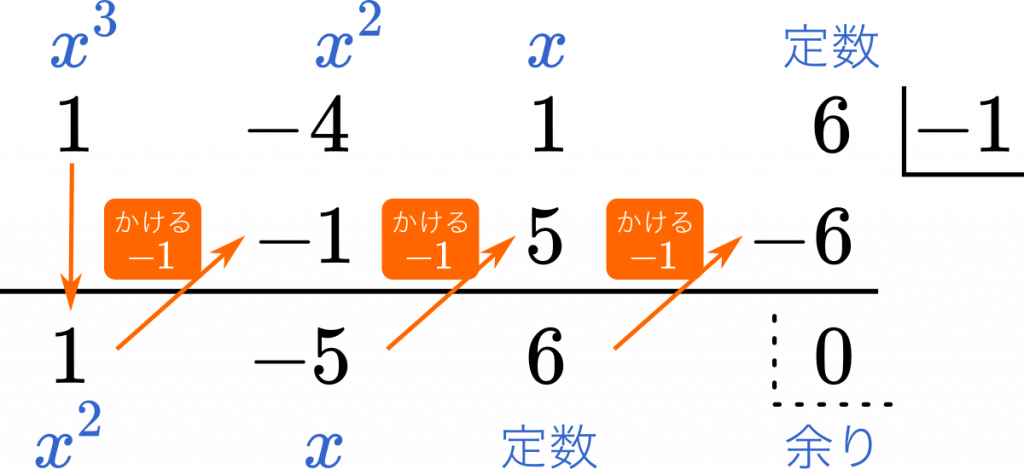
やり方としては，式の係数だけを並べて，$P(-1)=0$ なら $-1$ を右端に書いておきます。

最初は，左上の $1$ をそのまま下ろして，あとは $-1$ をかける，足し算，の繰り返しです。足し算の結果の部分が割り算の答えになりますが，上と下では次数が 1 つずれるところに注意しましょう。

なぜ，このような計算が成り立つのかについては，きちんと分からなくても大丈夫です。

ちなみに，ひっ算の場合と比べてみましょう。

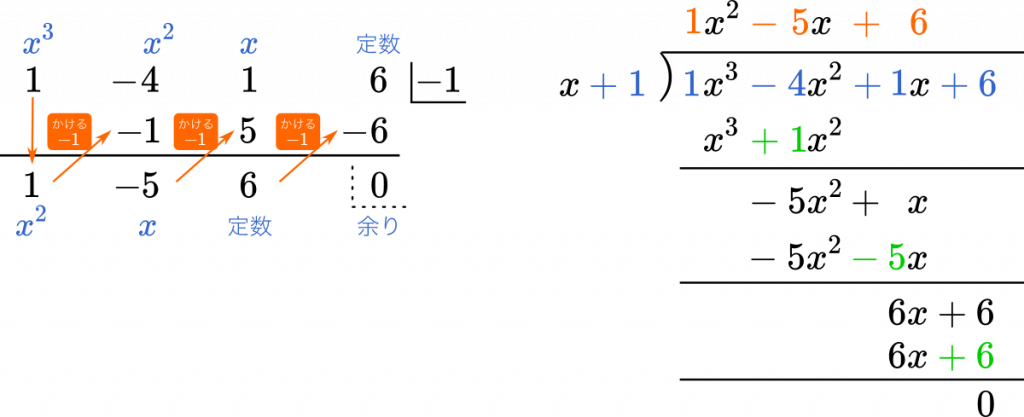
比べてみると分かりますが，組立除法はひっ算の係数の部分だけを取り出したものであることが分かります。ただし，ひっ算なら引き算するところを組立除法では足し算するので，符号が逆になる部分があることも分かると思います。

組立除法はひっ算の代わりにいつでも使えるわけではなく，割る数が $x-a$ の形になっているときだけです。

問題に戻りましょう。組立除法の結果

$P(x)=(x+1)(x^2-5x+6)$

あとは，普通に因数分解します。

$P(x)=(x+1)(x-2)(x-3)$ (答え)

このように，因数定理で 3 次以上の整式を因数分解することができます。理系の人は，あとあと数IIIでもこの計算が必要になるときがあるので，基本としてマスターしておきましょう。