【数II高次方程式】剰余の定理が成り立つ仕組みを掘り下げて考えてみる

剰余の定理が成り立つ仕組み

[例題] $x^3-3x^2+4$ を $x-1$ で割った余りを求めよ。

式をある値で割ったとき

式＝割る数×商＋余り

として表すことができます。

たとえば，$13=3\times4+1$ のような感じです。これは 13 を 3 で割ったとき，商は 4 で余りは 1 ということです。

同じように，問題文の式を書き直してみましょう。

$P(x)=x^3-3x^2+4=(x-1)Q(x)+R$

$Q(x)$ は商，$R$ は余りです。商は $x$ の値によって変わるので，$Q(x)$ のように表します。

$x=1$ のときの商は $Q(1)$，$x=2$ のときの商は $Q(2)$ と書きます。商は実際に割り算してみないと分からないので，正体不明の存在として $Q(x)$ と書きます。この $Q(x)$ は最後まで正体不明のままなので，剰余の定理がイマイチ納得できない原因になりやすいところです。

ここで，$x$ に 1 を代入します。

$P(1)=1^3-3\cdot1^2+4=(1-1)Q(1)+R$
$2=0\cdot Q(1)+R$
$2=R$

よって，余りは 2 です。(答え)

大事なポイントは $x=1$ とすると，$(1-1)Q(1)=0\cdot Q(1)=0$ となり $Q(x)$ の項が消去されるところです。

$Q(x)$ の値は割る数によって変わるので，どんな値になるか分かりません。そこで，0 のかけ算によって $Q(x)$ を消去することで，余り $R$ を求めようというわけです。

剰余の定理

上で見たように，$x=1$ とすると，余りの部分だけが残ります。つまり，$P(1)=R$ となります。
ここから剰余の定理が出来上がります。

分かりやすく言えば，$P(x)$ を $x-1$ で割った余りは，$P(1)$ で求められ，$P(x)$ を $x-3$ で割った余りは $P(3)$ で求められるということです。式に値を代入するだけで余りが分かる，という点では便利な定理です。

余りの性質

$R$ は定数です。これは，実際にひっ算で割ってみると分かります。

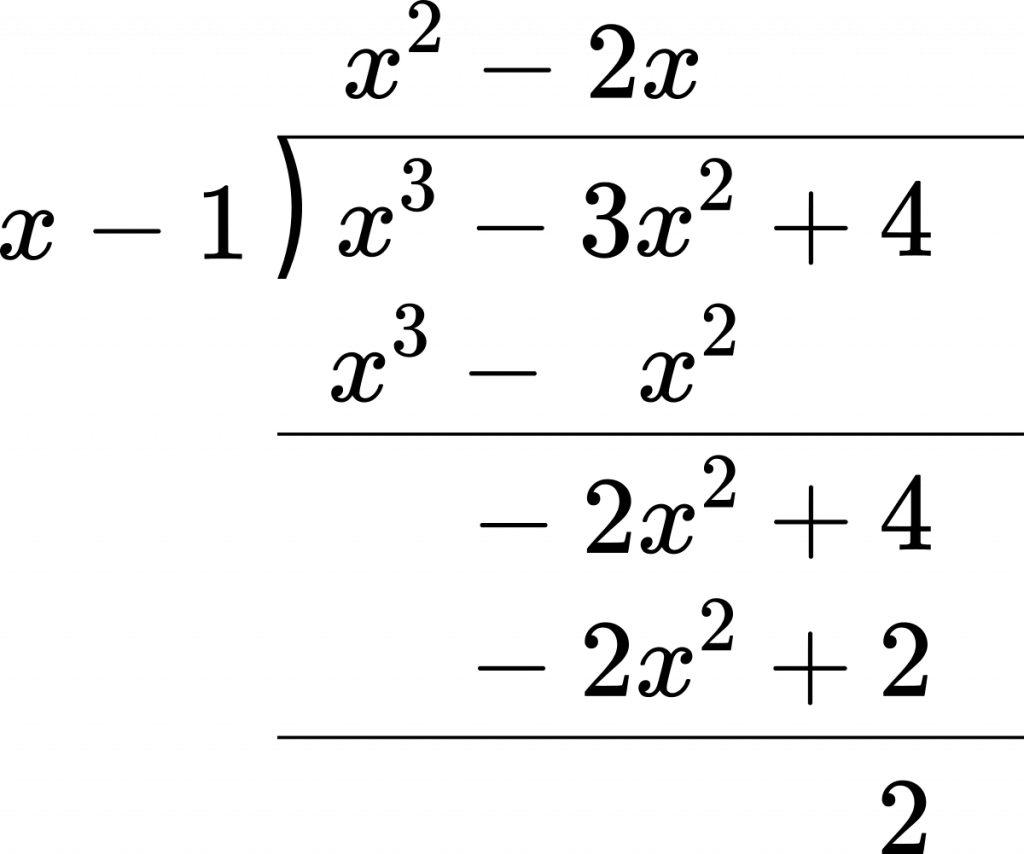
このように，割り算で $x^2$ の項まで消去することができ，定数だけが余りとして残ることが分かります。

別の例として，$2x^3-7x^2+8$ を $x^2-4x+3$ で割った場合を考えましょう。

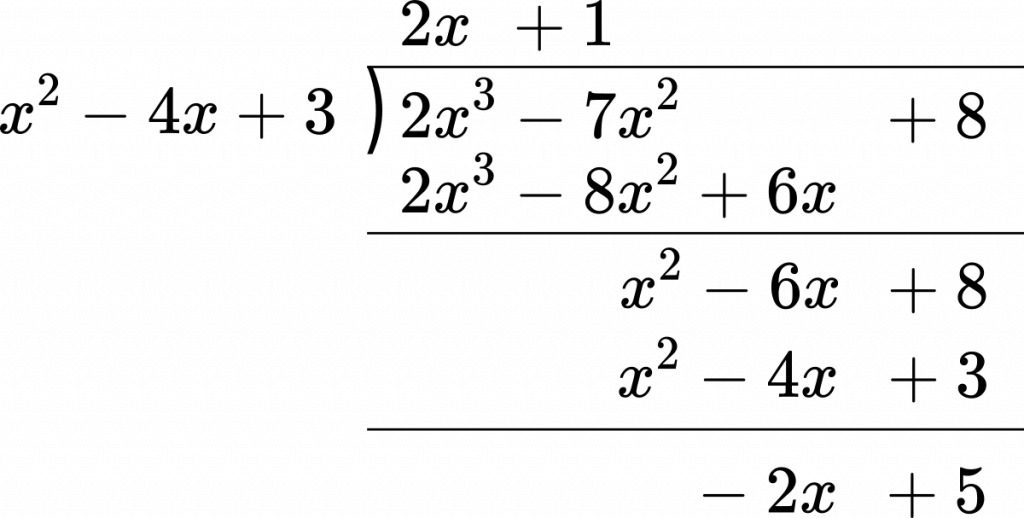
今度は，$x^2$ の項までは消去できましたが，$x$ の項以下は消去できませんでした。余りは $x$ の 1 次式です。

ここから，一つの法則が見えてきます。

・ある式を $x$ の 1 次式で割ると，その余りは定数となる。

・ある式を $x$ の 2 次式で割ると，その余りは $x$ の 1 次式（または定数）となる。

この法則を利用して，次の問題を考えてみましょう。

練習問題

[問題] 整式 $P(x)$ を $x-1$，$x+2$ で割った余りがそれぞれ $5$，$-1$ であるとき，$P(x)$ を $(x-1)(x+2)$ で割った余りを求めよ。

$(x-1)(x+2)=x^2+x-2$ だから，この式は $x$ の 2 次式です。そして，上で述べた法則から言えば，余りは $x$ の 1 次式（または定数）です。

いったん余りを $ax+b$ として，式を作ります。

$P(x)=(x-1)(x+2)Q(x)+ax+b$

剰余の定理を使いましょう。式を $x-1$ で割った余りが $5$ であるということは，$P(1)=5$ ということです。同様に，$P(-2)=-1$ が成り立ちます。

$P(1)=(1-1)(1+2)Q(x)+a\cdot1+b$
$=0\cdot Q(x)+a+b=a+b=5$

$P(-2)=(1+2)(-2+2)Q(x)+a(-2)+b$
$=0\cdot Q(x)-2a+b=-2a+b=-1$

よって

$a+b=5$ ・・・①
$-2a+b=-1$　・・・②

①－②

$3a=6$
$a=2$

①に代入して

$2+b=5$
$b=3$

したがって，求める余りは $2x+3$　（答え）

まとめ

剰余の定理は何のためにこのような計算をしているのか理解が難しいものです。ここでは，式を割った余りを求める上で剰余の定理が役立つことを示しました。

また，「割る数×商＋余り」の関係から，商の項を消去することで余りだけを取り出せることを学びました。

さらに，ある式をもう一つの式で割った場合，その余りは割る式の次数より一つ以上少ない次数となることが分かりました。

これらの考え方は，高次方程式を因数分解する際に役立ちます。