【数III複素数平面】複素数全体が円になる場合/複素数をx+yiに置き換える(北海道大2018理系第2問)

公開日:2020/10/28

最終更新日:2020/10/28

$z+\cfrac{4}{z}$ が実数となるような 0 と異なる複素数 $z$ の全体を $D$ とする。(北海道大2018)

(1) $D$ を複素数平面上に図示せよ。

(2) $k$ を実数とする。 $D$ に属する $z$ で方程式

$k\Big(z+\cfrac{4}{z}+8\Big)=i\Big(z-\cfrac{4}{z}\Big)$

を満たすものが存在するような $k$ の値の範囲を求めよ。ただし， $i$ は虚数単位を表す。

複素数全体が円になる

(1)から始めます。

与式が実数であるというところから，次の定義を思い出しましょう。

$z$ が実数のとき， $z=\bar{z}$ が成り立つ。

どういうこと？

たとえば，

z=1+3i

なら

\bar{z}=1-3i

だよね。これを共役な複素数と言う。でも，

z

が実数ということは，

z=1+0i=1

みたいな数になっている。このとき，

\bar{z}=1-0i=1

となって，

z=\bar{z}

が成り立つ。

虚数の部分が 0 ってことか。

$z+\cfrac{4}{z}=\Big(\overline{z+\cfrac{4}{z}}\Big)$
$z+\cfrac{4}{z}=\bar{z}+\cfrac{4}{\bar{z}}$

上の線の外し方どうしたらいいんですか？

これ，共役な複素数を表す記号で，一般的にバー(棒)って言ってる。バーはそれぞれに分解してよい。

$\Big(\overline{z+\cfrac{4}{z}}\Big)=\bar{z}+\cfrac{\bar{4}}{\bar{z}}$

そして，

\bar{4}=4

になる。虚数の部分のプラスマイナスを逆にするのが共役であって，実数の部分はそのままだったよね？だから，もともと虚部が無いものについては，そのままバーを外せば良い。

$z-\bar{z}=\cfrac{4}{\bar{z}}-\cfrac{4}{z}$

右辺を通分してまとめます。

$z-\bar{z}=\cfrac{4(z-\bar{z})}{z\bar{z}}$

両辺を $z-\bar{z}$ で割ると

$1=\cfrac{4}{z\bar{z}}$
$z\bar{z}=4$

公式 $z\bar{z}=|z|^2$ より

$|z|^2=4$
$|z|=2$ (答え)

ここは，目的を持って式変形するというよりは，似たような部分を適当にまとめていくうちに何となく出来上がってしまった，という感じです。

複素数をx+yiに置き換える

(2)に進みます。

これもまた，方向性が見えないので，とりあえず式を整理して考えることにしましょう。

$k\Big(z+\cfrac{4}{z}+8\Big)=i\Big(z-\cfrac{4}{z}\Big)$
$k\bar{z}+\cfrac{4k}{z}+8k=iz-\cfrac{4i}{z}$

移項して

$iz-k\bar{z}=\cfrac{4i}{z}+\cfrac{4k}{\bar{z}}+8k$

右辺を通分して

$=\cfrac{4(i\bar{z}+kz)}{z\bar{z}}+8k$

公式 $z\bar{z}=|z|^2$ より

$=\cfrac{4(i\bar{z}+kz)}{|z|^2}+8k$

(1)より $|z|^2=4$ だから

$=\cfrac{4(i\bar{z}+kz)}{4}+8k$
$=kz+i\bar{z}+8k$

移項して

$(k-i)z+(k+i)\bar{z}+8k=0$

で？

複素数平面の問題では，式を整理してもこれ以上どうしていいのか分からなくなるときがあります。

このとき， $z$ を $z=x+yi$ という形に置き換えるとうまくいくことがあります。同様に， $\bar{z}=x-yi$ としてみましょう。

$z=x+yi$ ， $\bar{z}=x-yi$ として

$(k-i)(x+yi)+(k+i)(x-yi)+8k=0$
$kx+kyi-xi+y+kx-kyi+xi+y+8k=0$
$2kx+2y+8k=0$
$kx+y+4k=0$

式が直線であることが分かりました。

そして，問題文から，この直線が $D$ に属する，つまり原点を中心とする半径 2 の円と重なる部分があればよい，ということになります。

共有点ができるということか。

ここから，数IIで習った円と直線の方程式の話に戻ります。

原点が中心である円とある直線が共有点を持つことと，直線と原点の距離 $d$ が 2 以下であることは同じでした。

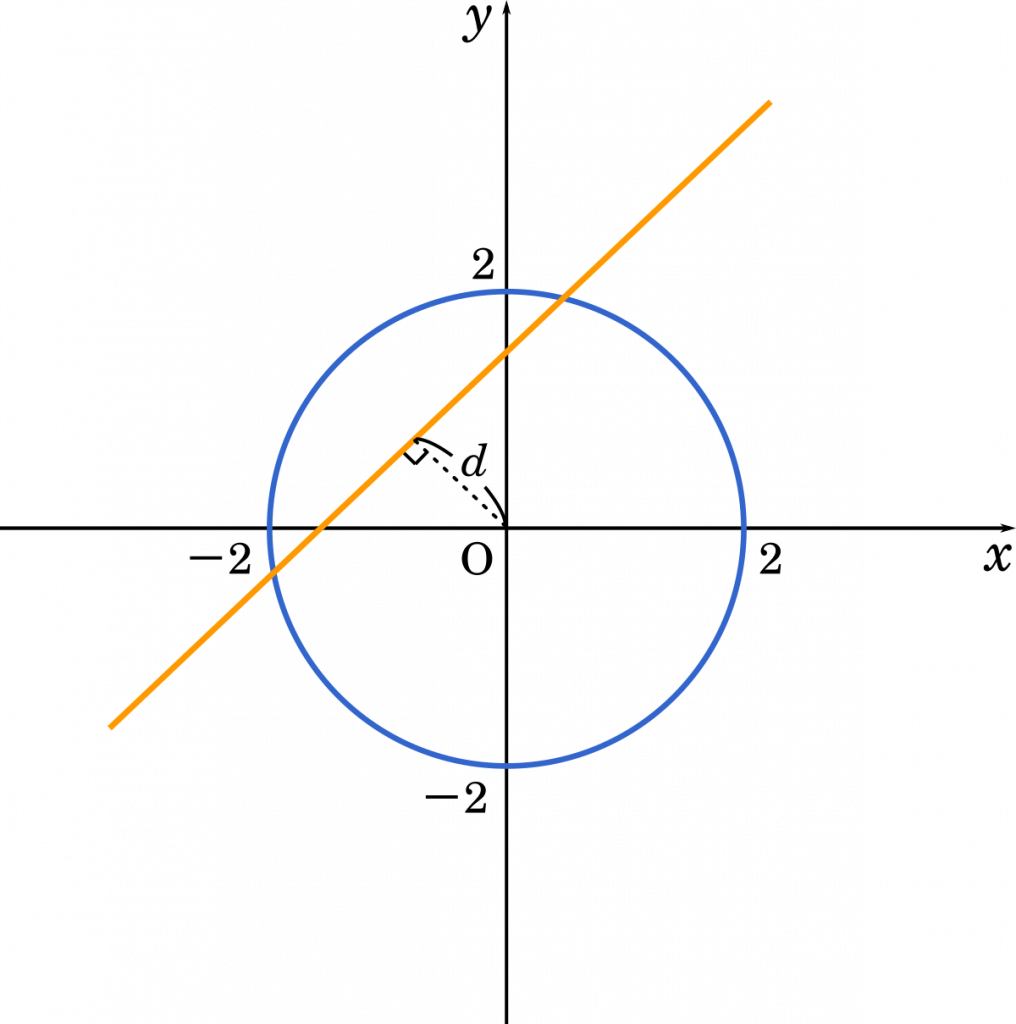
そこで，点と直線の距離の公式を用います。

点 $(x_1,y_1)$ と直線 $ax+by+c=0$ の距離 $d$ は
$d=\cfrac{|ax_1+by_1+c|}{\sqrt{a^2+b^2}}$

公式に当てはめると

$d=\cfrac{|k\cdot0+1\cdot0+4k|}{\sqrt{k^2+1^2}}$
$\cfrac{|4k|}{\sqrt{k^2+1}}\leqq2$

左辺は正の数です。よって，両辺を 2 乗しても不等号の向きは変わりません。

$\cfrac{16k^2}{k^2+1}\leqq4$
$16k^2\leqq4(k^2+1)$
$16k^2\leqq4k^2+4$
$12k^2\leqq4$
$k^2\leqq\cfrac{1}{3}$
$k^2-\cfrac{1}{3}\leqq0$
$\Big(k+\cfrac{1}{\sqrt{3}}\Big)\Big(k-\cfrac{1}{\sqrt{3}}\Big)\leqq0$
$-\cfrac{1}{\sqrt{3}}\leqq k\leqq\cfrac{1}{\sqrt{3}}$ (答え)

【数III複素数平面】複素数全体が円になる場合/複素数をx+yiに置き換える(北海道大2018理系第2問)

複素数全体が円になる

複素数をx+yiに置き換える

関連