【数III複素数平面】外接円の中心の存在範囲を求める(北海道大2017)

複素数平面上に 3 点 O，A，B を頂点とする △OAB がある。ただし，O は原点とする。△OAB の外心を P とする。3 点 A，B，P が表す複素数を，それぞれ $\alpha$，$\beta$，$\gamma$ とするとき，
$\alpha\beta=z$
が成り立つとする。(北海道大2017)

(1) 複素数 $\alpha$ の満たすべき条件を求め，点 A ($\alpha$) が描く図形を複素数平面上に図示せよ。

(2) 点 P ($z$) の存在範囲を求め，複素数平面上に図示せよ。

複素数が垂直二等分線になる

(1)から考えていきます。

ある三角形があったとして，その外接円の中心はどこにあるのでしょうか。それは外接円の性質を考えれば分かるはずです。

外接円を描いてみると，円の半径より OP = BP となることが分かります。よって

$|z|=|z-\beta|$

$z=\alpha\beta$ より

$|\alpha\beta|=|\alpha\beta-\beta|$
$|\alpha|\cdot|\beta|=|\beta|\cdot|\alpha-1|$
$|\alpha|=|\alpha-1|$

つまり

$|\alpha-0|=|\alpha-1|$

この形は垂直二等分線でした。

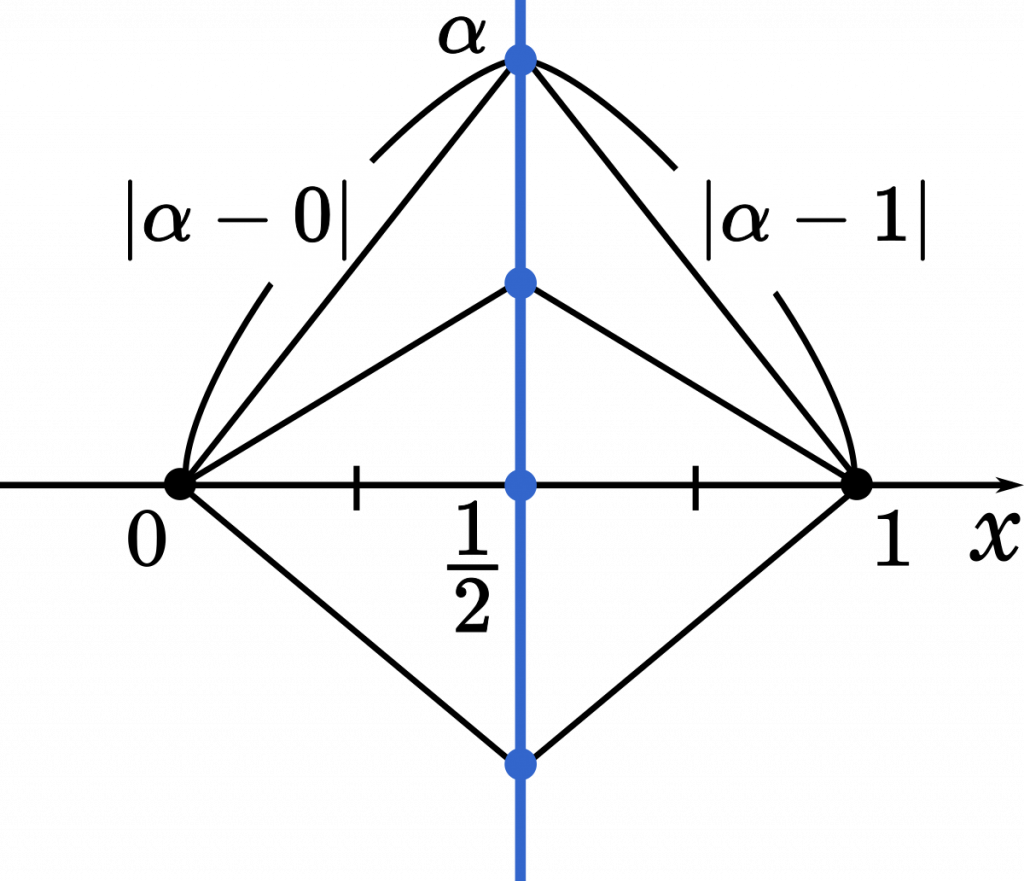
したがって，$\text{A}(\alpha)$ が描く図形は，点 0，1 を結ぶ垂直二等分線。(答え)

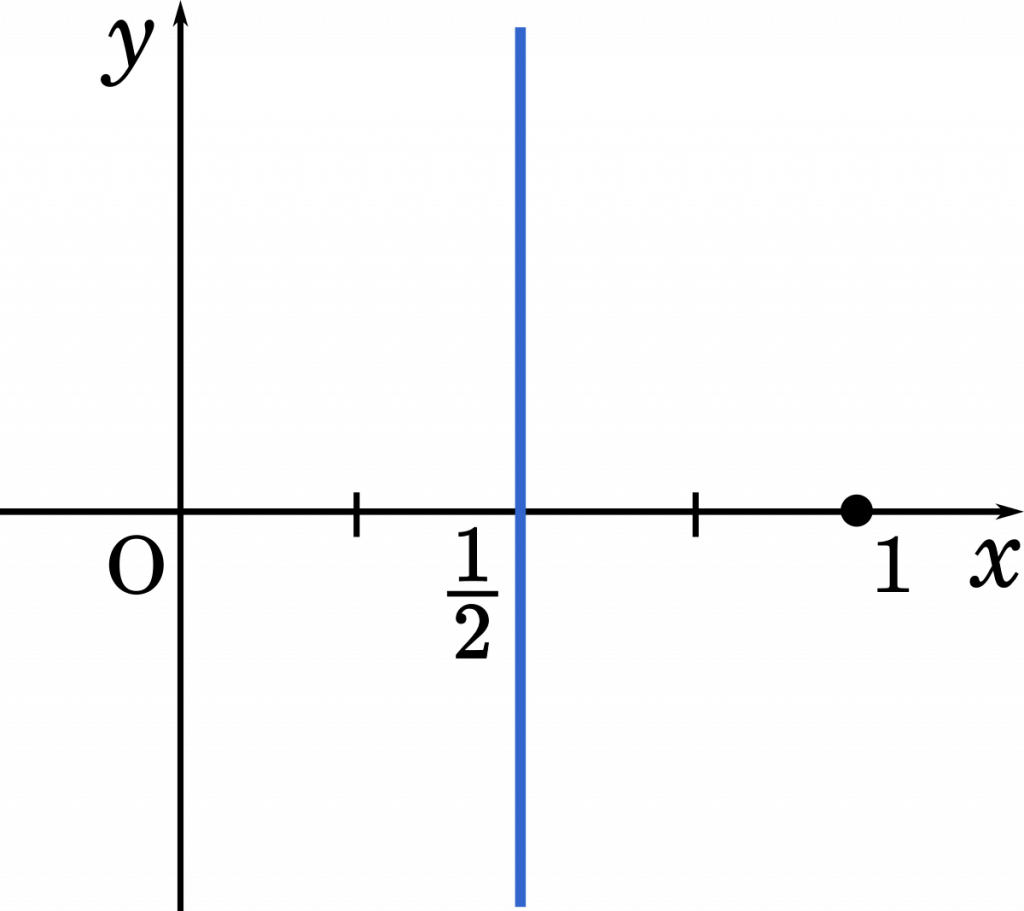
点 A，B をどの位置に置いたとしても外接円を作ることはできます。しかし，$\alpha\beta=z$ の関係から B，Z の位置が決まると A の位置もある 1 点に決まることが分かります。

問題文を読んだとき，普通ならば A，B の位置を決めて，それをもとに P の位置を決めるという順番で考えるはずです。

しかし，ここでは A の位置を問われているので，順番を入れ替えて B，P の位置から A の位置を求めるという計算を行っているのです。

ここで問われていることは発想の転換です。

円の中心の存在範囲を求める

(2)に進みます。

(1)で考察したことをもとにすると，今度は A，B の位置が決まれば，P の位置が 1 点に決まるはずです。

そして，さらに考えると，A，P の位置が決まれば，B の位置が 1 点に決まることになります。

OP = AP より
$|z|=|z-\alpha|$
$|\alpha\beta|=|\alpha\beta-\alpha|$
$|\alpha|\cdot|\beta|=|\alpha|\cdot|\beta-1|$
$|\beta|=|\beta-1|$

つまり，点 A と同様に点 B も点 0，1 を結ぶ垂直二等分線上です。

A，B の位置は分かりましたが，このままでは計算が進みません。このようなとき，$z$ を具体的に $z=x+yi$ とし，いったん複素数として表してみるとよいでしょう。

同様に，$\alpha$，$\beta$ も
$\alpha=\cfrac{1}{2}+si$
$\beta=\cfrac{1}{2}+ti$
としておきます。

文字が増えると不安になるものです。しかし，ゴール地点を見極めて，不要な文字が最終的に消去できるのであれば，実際のところ文字をどう定めても問題ではないのです。

ここから
$z=\alpha\beta$
$=\Big(\cfrac{1}{2}+si\Big)\Big(\cfrac{1}{2}+ti\Big)$
$=\cfrac{1}{4}+\cfrac{1}{2}(s+t)i-st$

実部と虚部で整理して

$=\cfrac{1}{4}-st+\cfrac{1}{2}(s+t)i$

よって

$x+yi=\cfrac{1}{4}-st+\cfrac{1}{2}(s+t)i$

左右を比べると

$x=\cfrac{1}{4}-st$ ・・・①
$y=\cfrac{1}{2}(s+t)$ ・・・②

①より
$st=-x+\cfrac{1}{4}$

②より
$s+t=2y$

このように和と積が出来上がったら，解と係数の関係を思い出しましょう。

解と係数の関係より
$X^2-2yX-x+\cfrac{1}{4}=0$

この二次関数に意味はありません。単に，$s$，$t$ を解に持つ二次関数というだけです。しかし，ここから $x$，$y$ の関係式を作ることができます。

$\cfrac{D}{4}=y^2-\Big(-x+\cfrac{1}{4}\Big)\geqq0$

点 A，B が存在するとき，$s$，$t$ はある実数として存在することになります。したがって，二次関数は異なる二つの実数解を持つはずです。

式を変形して
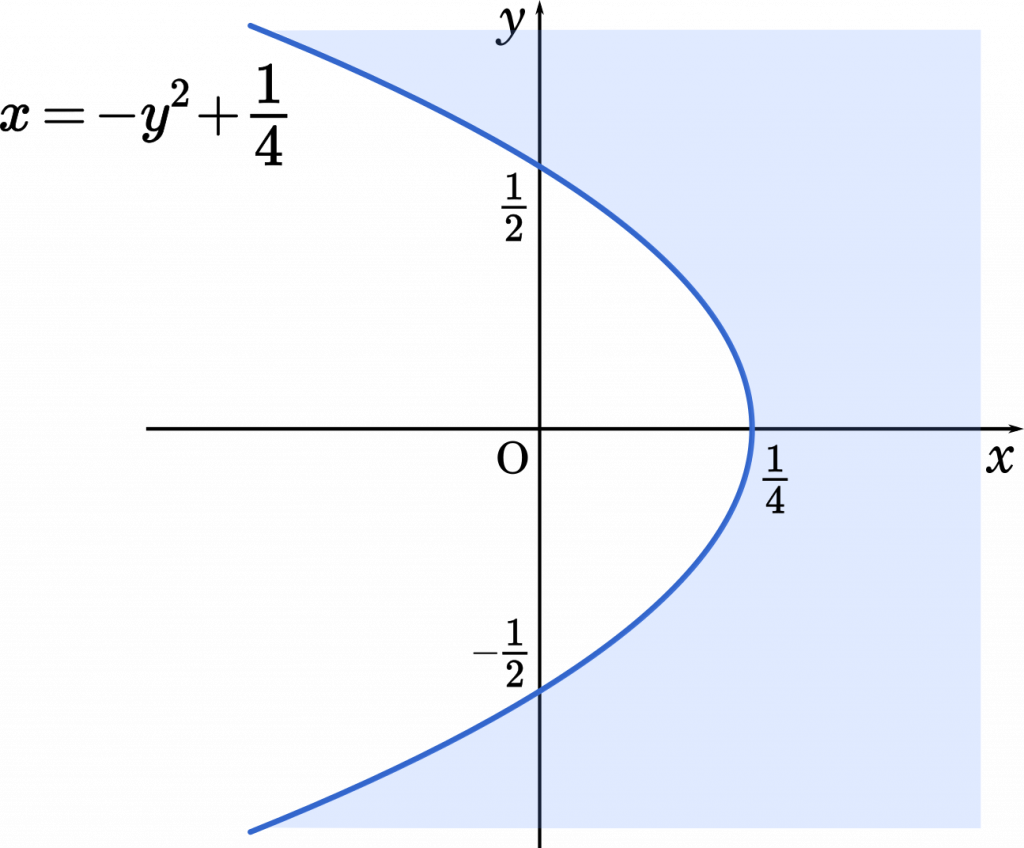
$x\geqq-y^2+\cfrac{1}{4}$

これで，求める $x$，$y$ の関係式が出来上がりました。

$x=-y^2+\cfrac{1}{4}$ は，$y=-x^2+\cfrac{1}{4}$ の $x$ と $y$ を入れ替えた式だと考えることができます。つまり逆関数です。

逆関数は，$x=y$ の直線において対称の関係にあるので，それぞれの点を対称移動させていくと，次のようなグラフになります。

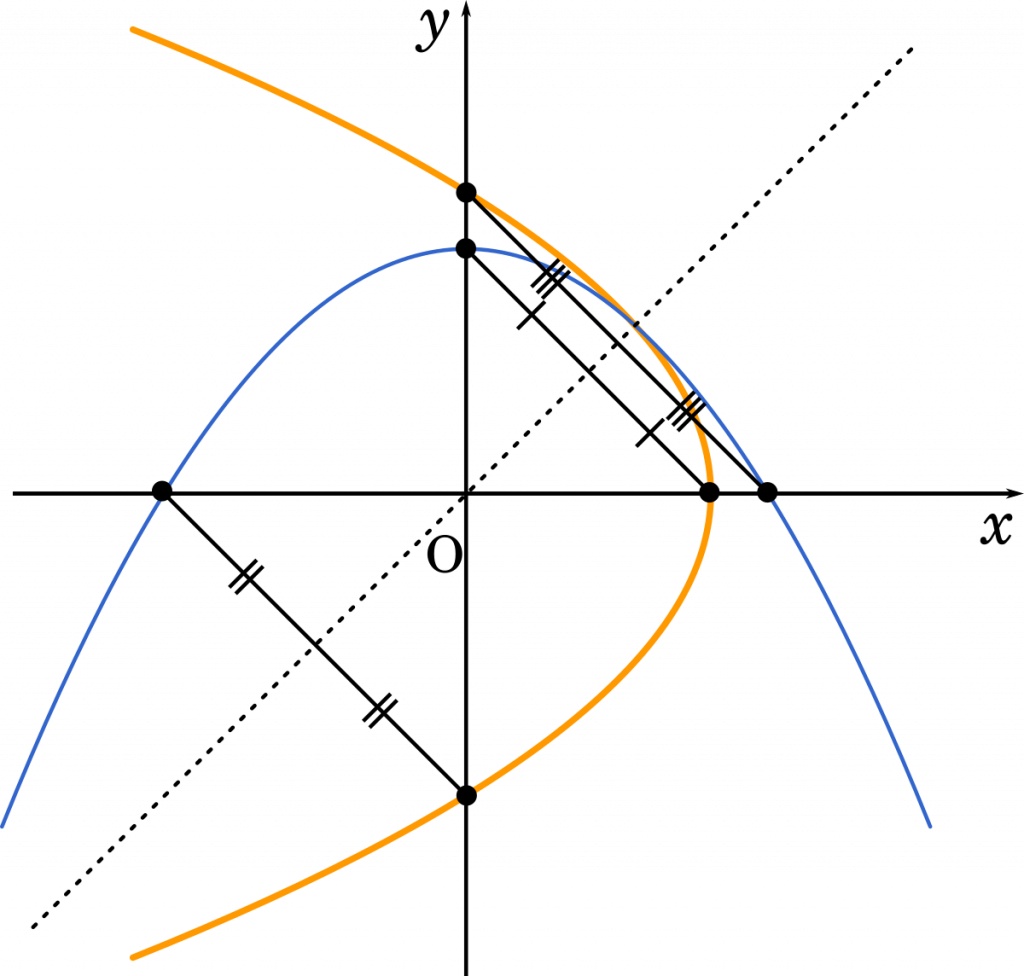
したがって，P($z$) の存在範囲は