【数IA図形】外接円と垂直に交わる直線(北海道大2018文系第1問)
$t>1$ とする。△ABC において AB=$\sqrt{t^2+1}$,BC=$t-1$,AC=$\sqrt{2}$ とし,点 O を△ABC の外心とする。
(1) ∠ACB の大きさを求めよ。
(2) 直線 CO と直線 AB が垂直に交わるときの $t$ の値を求めよ。
(北海道大2018)
余弦定理を用いる
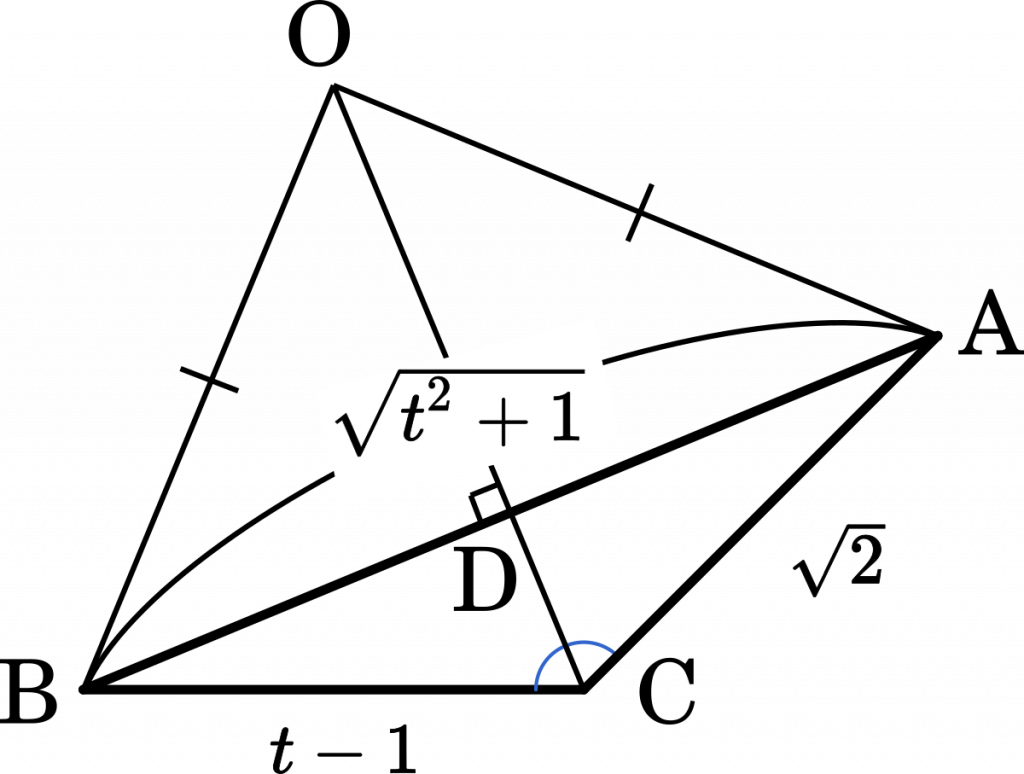
(1)から進めます。
3 辺の長さが分かっているので余弦定理を用いれば角の大きさを求めることができます。
余弦定理より
$(\sqrt{t^2+1})^2=(t-1)^2+(\sqrt{2})^2-2(t-1)\cdot\sqrt{2}\cos\angle\text{ACB}$
$t^2+1=t^2-2t+1+2-2\sqrt{2}(t-1)\cos\angle\text{ACB}$
$2\sqrt{2}(t-1)\cos\angle\text{ACB}=-2t+2$
$\cos\angle\text{ACB}=\cfrac{-(t-1)}{\sqrt{2}(t-1)}$
$=-\cfrac{\sqrt{2}}{2}$
$\angle\text{ACB}=\cfrac{3}{4}\pi$ (答え)
外接円の半径に注目する
(2)に進みます。
外接円の中心 O と A, B の間に直線を引くと,AO と BO は外接円の半径であり,AO = BO が成り立つことが分かります。
△AOD と △BOD は合同なので,結果的に AC = BC が成り立ちます。
△AOD と △BOD において
AO=BO
DO=DO
より,△AOD≡△BOD
よって,AD = BD
これより,同様に △ACD≡△BCD
$t-1=\sqrt{2}$
$t=\sqrt{2}+1$ (答え)
SNSでシェア