【数Ⅱ積分】どの文字を積分すればいいか分からない

正方形の面積を積分で示す

実際に解いてみましょう。

$\displaystyle\int_{0}^{x}{x}\enspace dx = \left[ \frac{1}{2}x^2 \right]_{0}^{x}$
$\displaystyle =\frac{1}{2}x^2-0=\frac{1}{2}x^2$

なぜ、$\displaystyle\frac{1}{2}x^2$ になってしまうのでしょうか？

式に $dx$ とあることから変化する値は $x$ です。 $x$ の値は $ 0$ から $x$ まで変化します。それを積み重ねたものが積分の結果になるから、結局この式は三角形の面積になるのです。

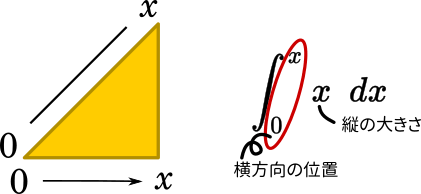
実はこの式にはもう少し問題があります。積分区間は定数でなければなりません。式の積分区間は $0$ から $ x $ となっており、$x$ を定数として扱っています。ところが、後ろの部分で $dx$ とすることで、$x$ を変化する値として定義しています。混乱の原因となるので、このような式の書き方はそもそも望ましくありません。

変化する文字と変化しない文字を区別する

では、どのように書けばいいのでしょうか？　要は0→xと変化していくときにタテの長さが変化しないようにしたいのです。

そこで、$x$ は変化しない値（定数）ということにして、変化する値を別の文字  $t$ とおいてみましょう。

イメージとしてはこういう感じです。

式はこうなります。

$\displaystyle\int_{0}^{x}{x}\enspace dt=\left[ xt\right]_0^x$
$=x^2-0$
$=x^2$

定数は数字と同じ扱いです。例えば、2 を x で積分したら 2x になるのと同じように、x を t で積分したら xt となるのです。

変化する文字は１つだけ、あとは定数扱い

ここで、積分計算における大事な原則を覚えましょう。

積分において、変化する文字は１つだけであり、その他の文字は常に定数扱いとする、ということです。

積分の式に dx と書いてあれば、積分の計算をするのは x だけで、他の文字を積分計算してはいけません。

この原則を知っておけば、積分計算で何を積分していいのか混乱することはなくなるはずです。

実際に例題で考える

$\displaystyle\int{(2x-y)^2}\enspace dy$
$\displaystyle =\int{4x^2-4xy+y^2}\enspace dy$

ここで、dy に注目しましょう。dy とは y について積分しろ という意味であり、x は定数と考えるので積分してはいけません。

よって

$=4x^2y-4x\cdot\frac{1}{2}y^2+\frac{1}{3}y^3$
$=4x^2y-y^2xy^2+\frac{1}{3}y^3+C$ (Cは積分定数）(答え)

どの文字を積分するのか？を意識することが大切

教科書で積分を習い始めたとき、x を積分計算するクセがついてしまいがちです。しかし、常に x で計算するとは限らないので、積分の式の最後についている dx や dy といった文字を見て、どの文字について積分するのか？を確認するようにしましょう。もし、式の最後に dy と書いてあったら x は定数として考えるところにも注意しましょう。