【数Ⅱ式と証明】二項定理は「箱からボールを選ぶ問題」として考える

二項定理は「箱から球を取る話」におきかえる

$(a+b)^2$ は $(a+b)(a+b)$ ということです。これを展開する場合、 $a^2+ab+ba+b^2$ という順番で展開していきます。これは言い換えればカッコの中から一つずつ文字を取り出していく作業をしているということになりますよね。

例えるならこういうことです。

箱が２つあったとして、その中に a と b という二つの球があったとします。それぞれの箱から球を１つずつ取り出すとき、b を１つ取り出す組み合わせはいくつあるでしょうか？

これは、a — b、b — a でひく場合になるので、２通りありますよね。

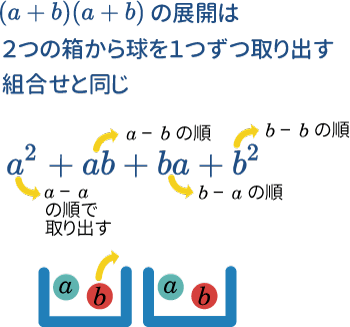
これをCを用いて表すと$_2C_1=2$となります。これは２個の箱から b を１個取る組合わせ、という意味です。

三乗の展開式の場合で考える

次に $(a+b)^3$ で考えましょう。これを展開したとき、 $ab^2$ の項の係数はいくらでしょうか？

式を書き替えると $(a+b)(a+b)(a+b)$ です。

これを展開するときも、$a ― a ― a、a ― a ― b、a ― b ― a、a ― b ― b$ …という感じでカッコの中から項を一つずつ取り出していきます。

このとき、今回は $ab^2$ の項だから３個の箱から b を２個取る組合せ、ということになります。

つまり、 $_3C_2=3$ （答え）です。

次数が増えても話は同じ

二項定理を使って展開式を書く

次に二項定理を使って$(a+b)^5$の展開式を書いてみましょう。

展開式はこうなります。

$_5C_0a^5b^0+_5C_1a^4b^1+_5C_2a^3b^2+_5C_3a^2b^3+_5C_4a^1b^4+_5C_5a^0b^5$

これをこのまま覚えようとしても意味が分からないですよね。そこで、いくつかのステップに分解して覚えていきましょう。

まず、a と b の部分を見ていきます。

５乗の式なら

① a は５でスタートして１つずつ減らす → 0 になったら終わり！

② b は 0 でスタートして１つずつ増やす → 5 になったら終わり！

となっているのが分かりますよね。

展開するときに、５つの箱から b を 0 個取る場合、1個取る場合、2個取る場合…と順番に書いていけばよいのです。反対に、合計で５つを取るのですから、b が 0 個なら a は 5つ取ることになるし、b が 1個なら a は4個取ることになります。だから a は1つずつ減っていくのです。

また、Cの部分は

① ５乗の式だから左下は5。

② 右下は 0 でスタートして１つずつ増やす → 5 になったら終わり！

上でやった通り、Cの部分はもし$ab^3$の項だったら「５つの箱から b を３つ取る組合せ」と考えて$_5C_3$とすればいいのです。

まとめ

(例題) $(a+b)^8$ の展開式を求めなさい。

８つの箱から b を 0個、１個、２個…８個取る組合せと考えて、

・係数の部分は、$_8C_0, _8C_1,_8C_2,\cdots, _8C_8$と順番に書いていく。

・項の部分は、b が 0 個なら反対に a は 8 個、b が 1 個なら反対に a は 7 個取るのだから、$a^8b^0, a^7b^1, a^6b^2,\cdots,a^0b^8$と書いていく。

$(a+b)^8$
$=_8C_0a^8b^0+_8C_1a^7b^1+_8C_2a^6b^2+_8C_3a^5b^3$
$\enspace\enspace+_8C_4a^4b^4+_8C_5a^3b^5+_8C_6a^2b^6+_8C_7a^1b^7$
$\enspace\enspace+_8C_8a^0b^8$
$_8C_0=_8C_8=1,\enspace_8C_5=_8C_3, \enspace _8C_6=_8C_2,$
$_8C_7=_8C_1,\enspace a^0=1, \enspace b^0=1$

だから

$=a^8+_8C_1a^7b+_8C_2a^6b^2+_8C_3a^5b^3$
$\enspace\enspace+_8C_4a^4b^4+_8C_3a^3b^5+_8C_2a^2b^6+_8C_1ab^7$
$\enspace\enspace+b^8$

$=a^8+8a^7b+28a^6b^2+56a^5b^3+70a^4b^4$
$\enspace\enspace+56a^3b^5+28a^2b^6+8ab^7+b^8$

(答え）