【スマホで読む・わかりやすい】センター数学IIB2020追試【解説・正解・問題】

第１問

正解と解説

ア,イ,ウエ　－, 8, 16　オカキ －20
ク 3　ケコ 16　サシ 14　ス 3
セ 2　ソ 6　タ,チ 3,2　ツ,テ 3,3
ト 3　ナ,ニ 2,3　ヌ 3　ネ,ノ 2,3
ハ 0　ヒ 3　フ 7　ヘ 6　ホ 3

〔1〕(1)

$y=-2^{2x}+2^{x+4}-48$ を変形すると

$y=-(2^x)^2+2^x\cdot2^4-48$

$t=2^x$ とおくと

$y=-t^2+16t-48$

式を平方完成すると

$y=-(t^2-16t)-48$
$=-(t-8)^2+64-48$
$=-(t-8)^2+16$

・・・アイウエ

$x=1$ のとき，$t=2^1=2$ だから

$y=-(2-8)^2+16=-20$

・・・オカキ

$x\geqq1$ のときの $t$ の値を考えると
$x=1$ のとき $t=2$ だから

$x\geqq1$ のとき

$t\geqq2^1$
$t\geqq2$

$y=-(t-8)^2+16$ は $t=8$ で最大値 $16$ をとる。

$t=8$ のとき

$8=2^x$
$x=3$

となるので，$y$ は $x=3$ で最大値 16 をとる。

・・・クケコ

〔1〕(2)

$1\leqq x\leqq k$ のとき

$2^1\leqq 2^x\leqq2^k$
$2\leqq t\leqq2^k$

(i) $2\leqq t<14$ のとき

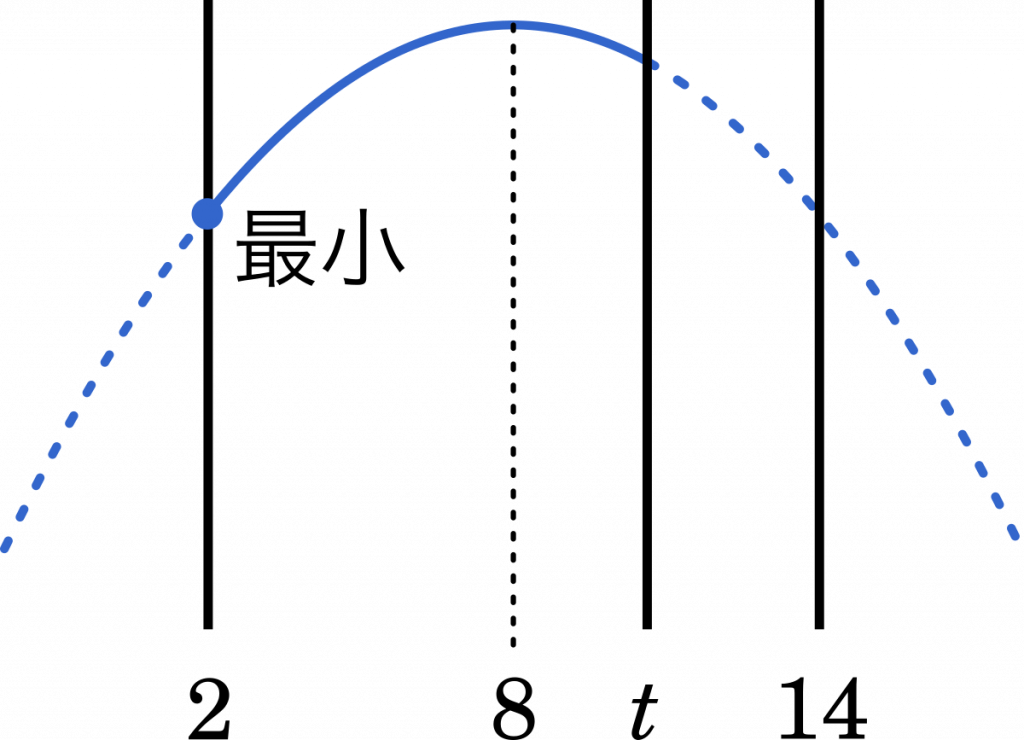
$t=2$ で最小値 $-20$ をとる。

(ii) $t=14$ のとき

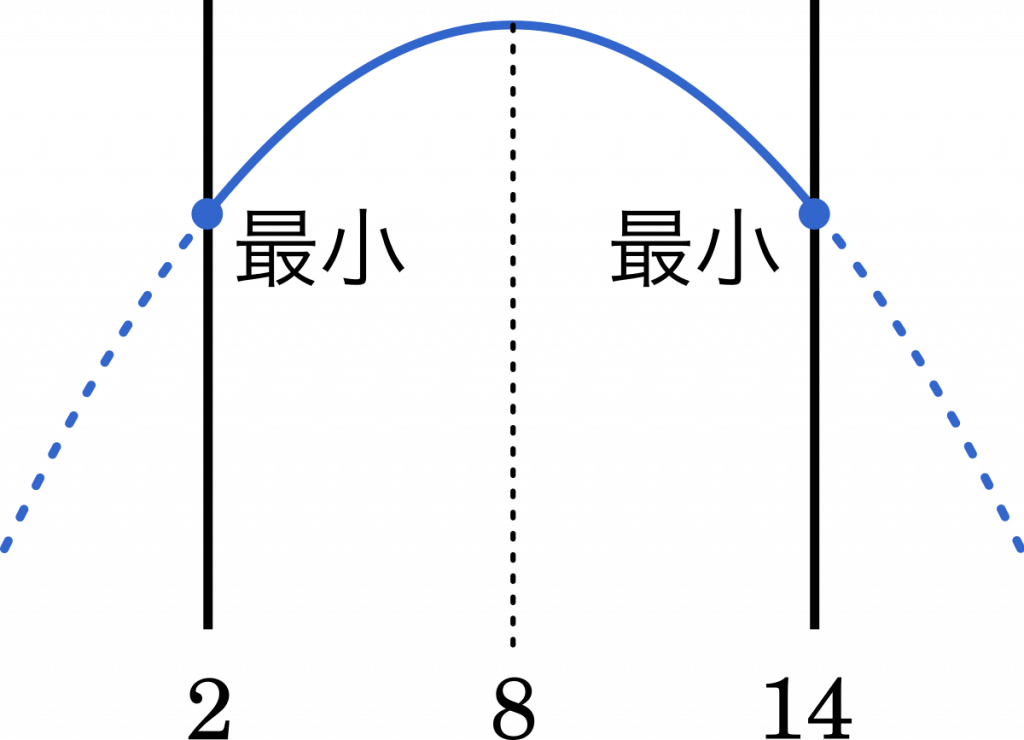
$t=2,14$ で最小値 $-20$ をとる。

(iii) $t>14$ のとき

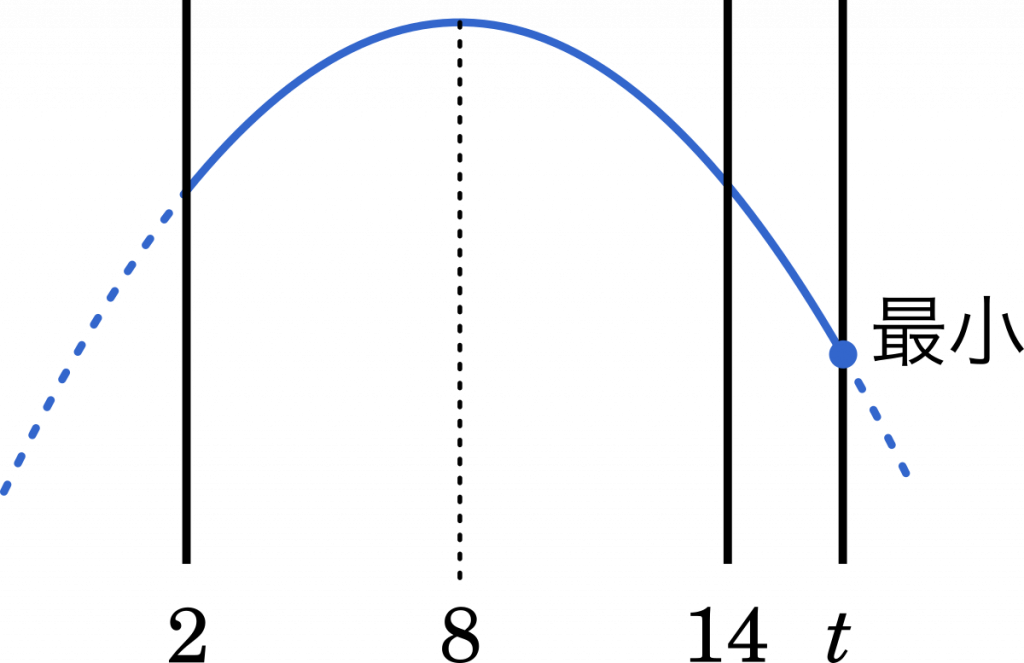
最小値は $-20$ より小さくなるので，不適。

よって，最小値が $-20$ となるのは

$2\leqq t\leqq14$

のときである。

ここで，$2\leqq t\leqq 2^k$ だから

$2\leqq2^k\leqq14$

が成り立つ。

底を 2 として，対数をとると

$\log_22\leqq\log_22^k\leqq\log_214$
$\log_22\leqq k\log_22\leqq\log_214$

$\log_22=1$ だから

$1\leqq k\leqq\log_214$

・・・サシ

ここで，$\log_214$ の値を考える。

$2^3<14<2^4$ より，それぞれ対数をとると

$\log_22^3<\log_214<\log_22^4$
$3\log_22<\log_214<4\log_22$
$3<\log_214<4$

したがって，範囲に含まれる最大の整数の値は 3 である。

・・・ス

〔1〕(3)

$0=-(t-8)^2+16$ とおくと

$(t-8)^2=16$
$t-8=\pm4$
$t=8\pm4$
$t=4,12$

$t=2^x$ より，$4=2^x$ とすると

$x=2$

また，$t=12$ とすると，$x$ の値は $t=4$ のときより大きくなるので，小さい方の $x$ の値は 2 である。

・・・セ

さらに，$t=12$ のときを考えると

$12=2^x$

となる。これを対数として表すと

$x=\log_212$

式を変形して

$=\log_2(3\cdot4)$ $\log_23+\log_24$
$=\log_23+2$

底の変換公式を用いて，底を 10 にすると

$=\cfrac{\log_{10}3}{\log_{10}2}+2$
$=\cfrac{0.4771}{0.3010}+2$
$=3.5\cdots$

したがって，⑥が適する。

・・・ソ

〔2〕(1)

$f(x)=\sqrt{3}\cos\Big(3x+\cfrac{\pi}{3}\Big)+\sqrt{3}\cos3x$

加法定理を用いると

$=\sqrt{3}\Big(\cos3x\cos\cfrac{\pi}{3}-\sin3x\sin\cfrac{\pi}{3}\Big)+\sqrt{3}\cos3x$
$=\sqrt{3}\Big(\cfrac{1}{2}\cos3x-\cfrac{\sqrt{3}}{2}\sin3x\Big)+\sqrt{3}\cos3x$
$=\cfrac{\sqrt{3}}{2}\cos3x-\cfrac{3}{2}\sin3x+\sqrt{3}\cos3x$
$=-\cfrac{3}{2}\sin3x+\cfrac{3\sqrt{3}}{2}\cos3x$

・・・タチツテ

三角関数の合成を用いて

$f(x)=3\sin\Big(3x+\cfrac{2}{3}\pi\Big)$

・・・トナニ

したがって，$f(x)$ は $3x+\cfrac{2}{3}\pi=\cfrac{\pi}{2}$ のときに，最大値 3 をとる。

・・・ヌ

次に，式を変形すると

$f(x)=3\sin3\Big(x+\cfrac{2}{9}\pi\Big)$

となり，グラフは以下のようになる。

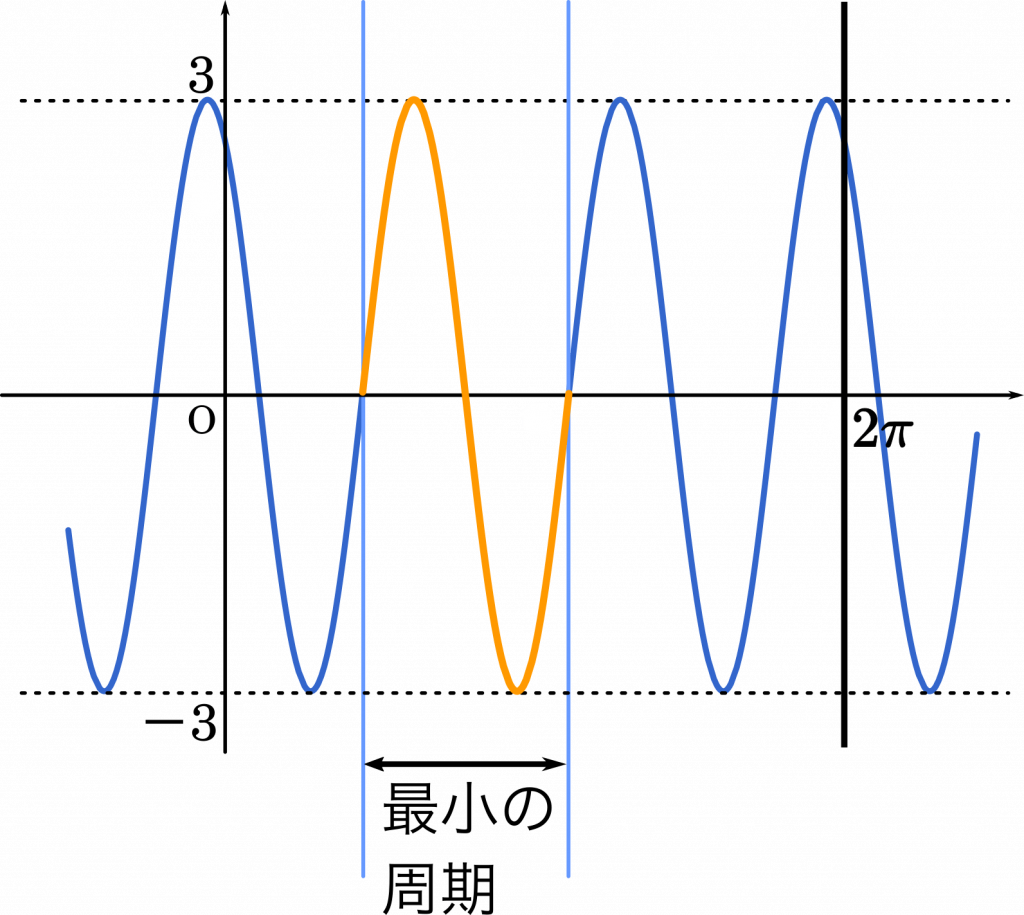
これは，$y=\sin x$ のグラフの縦方向の大きさを 3 倍，周期を $\cfrac{1}{3}$ 倍して，水平方向に$-\cfrac{2}{9}\pi$ 平行移動したものである。

関数の繰り返し部分を切り取ったものを周期という。周期はさまざまな大きさとして切り取ることができる（たとえば，最小のものの２，３・・・倍のように）。一般的に繰り返し部分が最も小さくなるように切り取ったものを周期を呼んでいる。さらに，グラフの正の側（$y$軸の右側）で切り取ったものが，正の周期のうち最小である。

$y=\sin x$ の周期は $2\pi$ だから，それを $\cfrac{1}{3}$ 倍するとよい。したがって，$f(x)$ の正の周期のうち最小のものは $\cfrac{2}{3}\pi$ である。

・・・ネノ

〔2〕(2)

(i) $|t|>3$ のとき

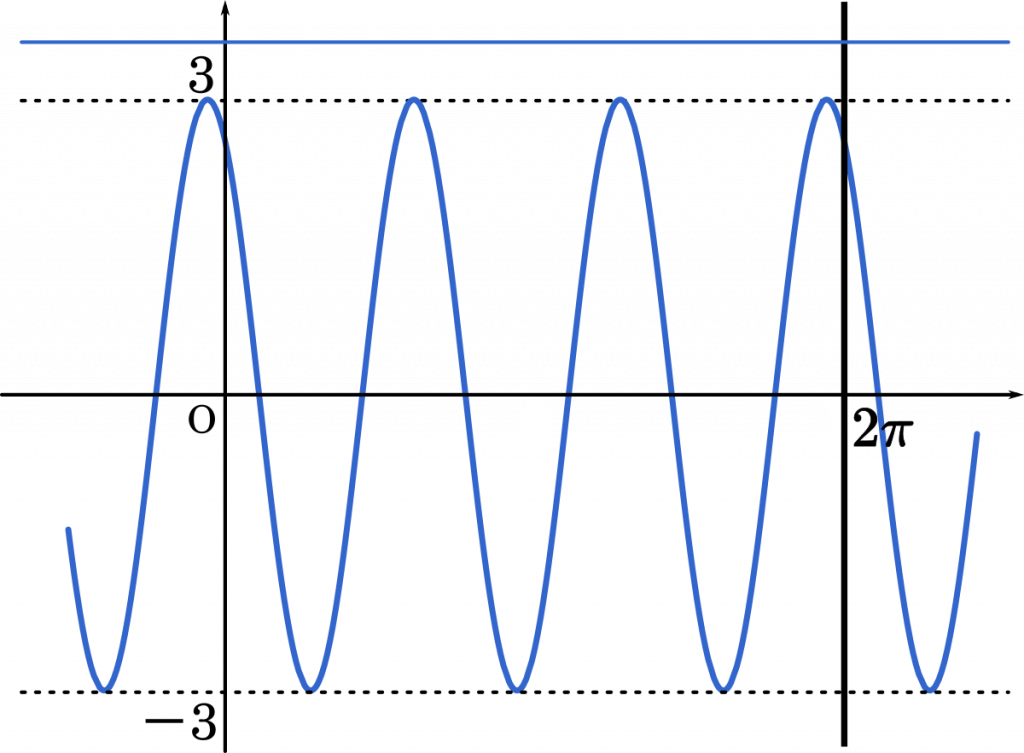
$t$ の範囲は $-3\leqq t\leqq3$ だから，グラフ上にあてはまる点は存在しない。したがって，$N=0$

・・・ハ

(ii) $t=3$ のとき

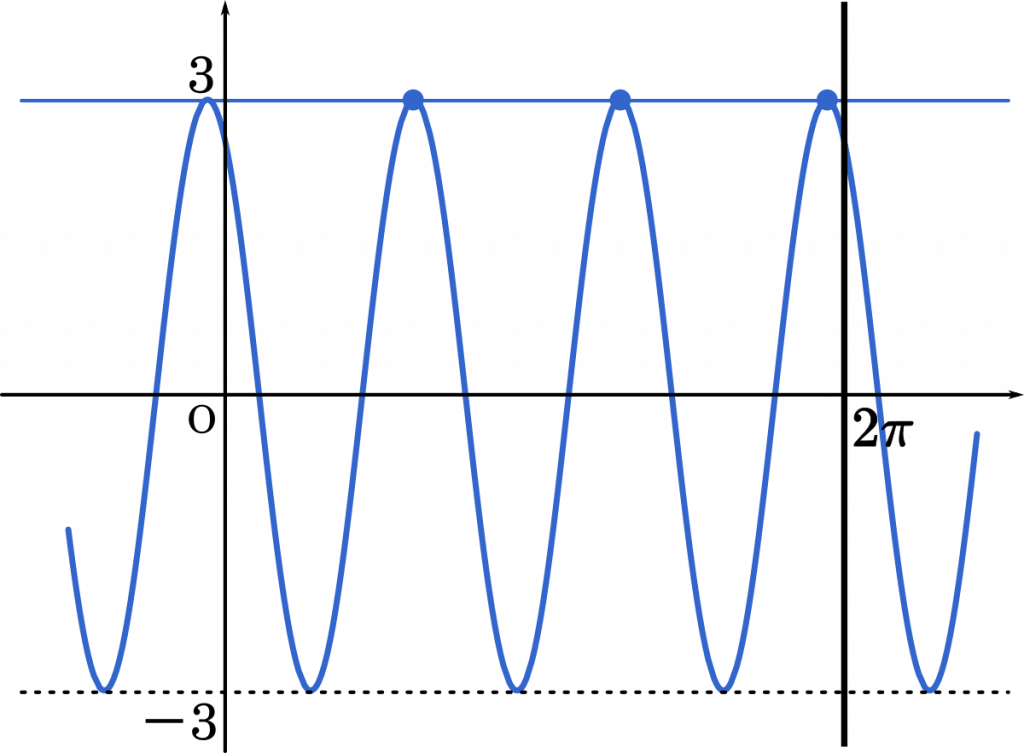
グラフより，$N=3$

・・・ヒ

(iii) $t=f(0)$ のとき

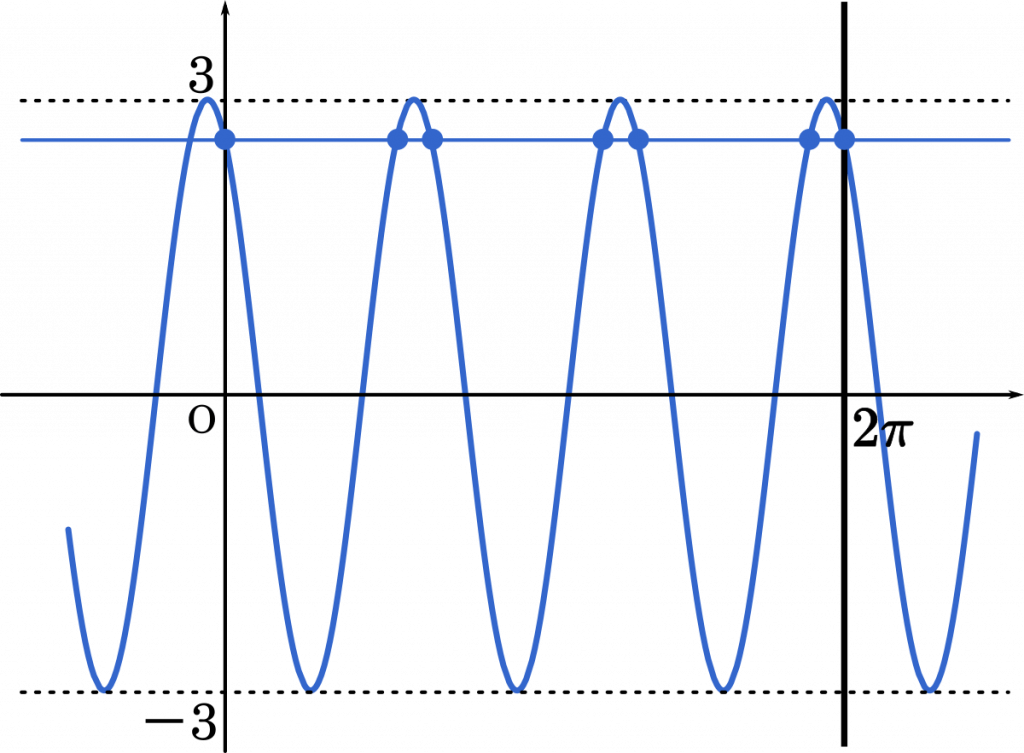
グラフより，$N=7$

・・・フ

(iv) $|t|<3$ かつ $t\not=f(0)$ のとき

$t$ はさまざまな値を取り得るので，条件に当てはまる任意の数をいったん 1 つ決めたうえで考えるとよい。

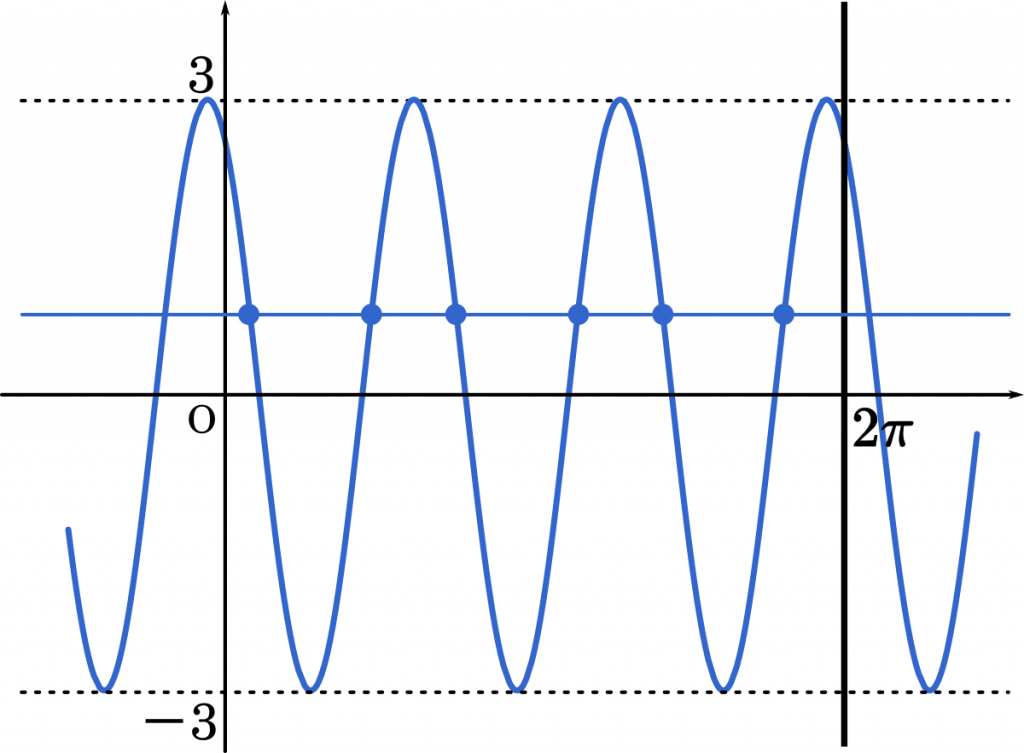
グラフより，$N=6$

・・・ヘ

(v) $t=-3$ のとき

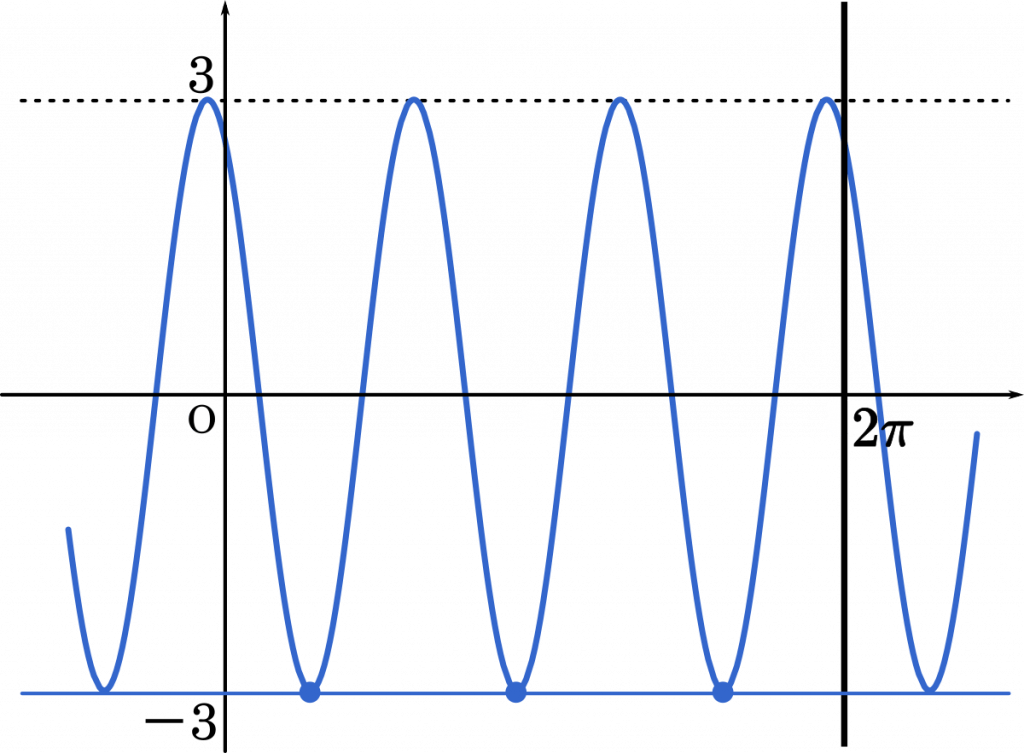
グラフより，$N=3$

・・・ホ

問題文

〔１〕　関数 $y=-2^{2x}+2^{x+4}-48$ について考える。

(1) $t=2^x$ とおく。$y$ を $t$ の式で表すと
$y=\boxed{\text{ ア }}(t-\boxed{\text{ イ }})^2+\boxed{\text{ ウエ }}$
となる。

　$x=1$ のとき，$y=\boxed{\text{ オカキ }}$ である。$x\geqq 1$ のときは，$y$ は $x=\boxed{\text{ ク }}$ で最大値 $\boxed{\text{ ケコ }}$ をとる。

(2) $k>1$ とする。$x$ が $1\leqq x\leqq k$ の範囲を動くとき，$y$ の最小値が $\boxed{\text{ オカキ }}$ であるような $k$ の値の範囲は
$1< k\leqq\log_2 \boxed{\text{ サシ }}$
である。この範囲に含まれる最大の整数の値は $\boxed{\text{ ス }}$ である。

(3) $y=0$ を満たす $x$ は二つある。そのうちの小さい方は $\boxed{\text{ セ }}$ である。また，大きい方は $\boxed{\text{ ソ }}$ を満たす。$\boxed{\text{ ソ }}$ に当てはまるものを，次の⓪～⑨のうちから一つ選べ。ただし，$\log_{10}2=0.3010,\log_{10}3=0.4771$ とする。

⓪ $1 < x < 1.2$　① $1.2 < x < 1.3$
② $1.5 < x < 1.6$　③ $2.4 < x < 2.5$
④ $2.5 < x < 2.6$　⑤ $2.6 < x < 2.8$
⑥ $3.5 < x <3.6$　⑦ $3.6 < x < 3.8$
⑧ $4.2 < x < 4.4$　⑨ $x > 10$

〔２〕 関数 $f(x)=\sqrt{3}\cos\Big(3x+\cfrac{\pi}{3}\Big)+\sqrt{3}\cos3x$ について考える。

(1) 三角関数の加法定理および合成を用いると

$f(x)=-\cfrac{\boxed{\text{ タ }}}{\boxed{\text{ チ }}}\sin3x+\cfrac{\boxed{\text{ ツ }}\sqrt{\boxed{\text{ テ }}}}{\boxed{\text{ チ }}}\cos3x$

$=\boxed{\text{ ト }}\sin\Big(3x+\cfrac{\boxed{\text{ ナ }}}{\boxed{\text{ ニ }}}\space\pi\Big)$

と表される。ただし，$0 < \cfrac{\boxed{\text{ ナ }}}{\boxed{\text{ ニ }}}\space\pi\leqq2\pi$ とする。

　したがって，$f(x)$ の最大値は $\boxed{\text{ ヌ }}$ である。また，$f(x)$ の正の周期のうち最小のものは $\cfrac{\boxed{\text{ ネ }}}{\boxed{\text{ ノ }}}\space\pi$ である。

(2) $f(x)$ を $0\leqq x\leqq2\pi$ の範囲で考えたとき，実数 $t$ に対して $f(x)=t$ となる $x$ の値の個数 $N$ を調べよう。$3x+\cfrac{\boxed{\text{ ナ }}}{\boxed{\text{ ニ }}}\space\pi$ のとり得る値の範囲に注意すると，次のことがわかる。

$|t| > \boxed{\text{ ヌ }}$ のとき，$N=\boxed{\text{ ハ }}$ である。

$t=\boxed{\text{ ヌ }}$ のとき，$N=\boxed{\text{ ヒ }}$ である。

$t=f(0)$ のとき，$N=\boxed{\text{ フ }}$ である。

$|t| < \boxed{\text{ ヌ }}$ かつ $t\not=f(0)$ のとき，$N=\boxed{\text{ ヘ }}$ である。

$t=-\boxed{\text{ ヌ }}$ のとき，$N=\boxed{\text{ ホ }}$ である。