【スマホで読む・わかりやすい】センター数学IA2020追試【解説・正解・問題】
第1問
正解と解説
アイ 36 ウエ 38 オ 6
カキ 50 クケ 26
コ,サ,シス,セ 5,2,26,2
ソタ,チ -4,6
ツ 3 テ 0
トナ,ニ,ヌ -1,4,2
ネ 2 ノ 8
ハヒ,フヘ -2,16
〔1〕
$(19+5\sqrt{13})(19-5\sqrt{13})$
$=361-325=36$
・・・アイ
$19+5\sqrt{13}$ の正の平方根を $\alpha$ とすると
$\alpha=\sqrt{19+5\sqrt{13}}$
$19-5\sqrt{3}$ の正の平方根を $\beta$ とすると
$\beta=\sqrt{19-5\sqrt{13}}$
となるので
$\alpha^2+\beta^2=19+5\sqrt{13}+19-5\sqrt{13}$
$=38$
・・・ウエ
$\alpha\beta=\sqrt{19+5\sqrt{13}}\times\sqrt{19-5\sqrt{13}}$
$=\sqrt{(19+5\sqrt{13})(19-5\sqrt{13})}$
$=\sqrt{361-325}=\sqrt{36}$
$=6$
・・・オ
$(\alpha+\beta)^2=\alpha^2+\beta^2+2\alpha\beta$
$=38+2\times6=50$
・・・カキ
$(\alpha-\beta)^2=\alpha^2+\beta^2-2\alpha\beta$
$=38-2\times6=26$
・・・クケ
さらに
$(\alpha+\beta)^2=50$ より
$\alpha+\beta=\pm\sqrt{50}=\pm5\sqrt{2}$
$\alpha,\beta$ はともに正の平方根だから
$\alpha+\beta=5\sqrt{2}$
また
$(\alpha-\beta)^2=26$ より
$\alpha-\beta=\pm\sqrt{26}$
ここで $\alpha-\beta$ が正の値か負の値かを考える。
$19+5\sqrt{13}>19-5\sqrt{13}$ だから
$\sqrt{19+5\sqrt{13}}>\sqrt{19-5\sqrt{13}}$
$\alpha>\beta$
となるので $\alpha-\beta$ は正の実数である。
よって,$\alpha-\beta=\sqrt{26}$
$\alpha+\beta=5\sqrt{2}$ と $\alpha-\beta=\sqrt{26}$ を連立すると
$2\alpha=5\sqrt{2}+\sqrt{26}$
$\alpha=\cfrac{5\sqrt{2}+\sqrt{26}}{2}$
・・・コサシスセ
これを $\alpha+\beta=5\sqrt{2}$ に代入すると
$\cfrac{5\sqrt{2}+\sqrt{26}}{2}+\beta=5\sqrt{2}$
$\beta=5\sqrt{2}-\cfrac{5\sqrt{2}+\sqrt{26}}{2}$
$=\cfrac{10\sqrt{2}-5\sqrt{2}-\sqrt{26}}{2}=\cfrac{5\sqrt{2}-\sqrt{26}}{2}$
〔2〕(1)
$p\implies q$ が真のときを考えると
$|x-a|>3$ は
$x-a\geqq 0$ のとき
$x-a>3$
$x>3+a$
$x-a<0$ のとき
$-x+a>3$
$-x>3-a$
$x<-3+a$
よって
$3+a<x<-3+a$

$p\implies q$ が真であるとき,$q$ の範囲は $p$ よりも広い。
したがって
$3+a<-1$
$a<-4$
・・・ソタ
$3<-3+a$
$6<a$
・・・チ
〔2〕(2)
$a=6$ のとき
$q:|x-6|>3$
となる。
ここで,$p:-1\leqq x\leqq 3$ であることに注意して,$x$ の値のうち,$p$ に当てはまらないものを考えると
$x=3$ のとき
$|3-6|>3$
$3>3$
となり,矛盾する。したがって,$x=3$ は命題「$p\implies q$」の反例である。
・・・ツ
〔2〕(3)
$a=1$ のとき
$q:|x-1|>3$
となる。
$x-1\geqq0$ のとき
$x-1>3$
$x>4$
また,$x-1<0$ のとき
$-x+1>3$
$-x>2$
$x<-2$
よって,$q$ は「$x<-2$ または $x>4$」だから
$\bar{q}:-2\leqq x\leqq4$
となる。さらに
$\bar{p}:x<-1$ または $x>3$ だから

$\bar{p}$ かつ $\bar{q}$ : $-2\leqq x<-1$ または $3<x\leqq4$
よって,「$\bar{p}$ かつ $\bar{q}$」$\implies r$ は偽。$r\implies$ 「$\bar{p}$ かつ $\bar{q}$」は真。
したがって,$a=1$ のとき,条件「$\bar{p}$ かつ $\bar{q}$」は条件 $r$ であるための必要条件であるが,十分条件ではない。
・・・テ
〔3〕(1)
式を展開すると
$f(x)=(x-a)(x-4)+4$
$=x^2-(a+4)x+4a+4$
式を平方完成すると
$=\Big(x-\cfrac{a+4}{2}\Big)^2-\cfrac{(a+4)^2}{2}+4a+4$
$=\Big(x-\cfrac{a+4}{2}\Big)^2-\cfrac{a^2+8a+16-16a-16}{4}$
$=\Big(x-\cfrac{a+4}{2}\Big)^2-\cfrac{a^2-8a}{4}$
$=\Big(x-\cfrac{a+4}{2}\Big)^2-\cfrac{a^2}{4}+2a$
したがって,$y=f(x)$ の最小値は
$\cfrac{-1}{4}a^2+2a$
・・・トナニヌ
〔3〕(2)
$a-2\leqq x\leqq a+2$ における最大値を求めると
$f(x)=(x-a)(x-4)+4$ より
$f(a)=4,f(4)=4$ となる
$a$ は 4 以上の定数であることに注意してグラフを描くと
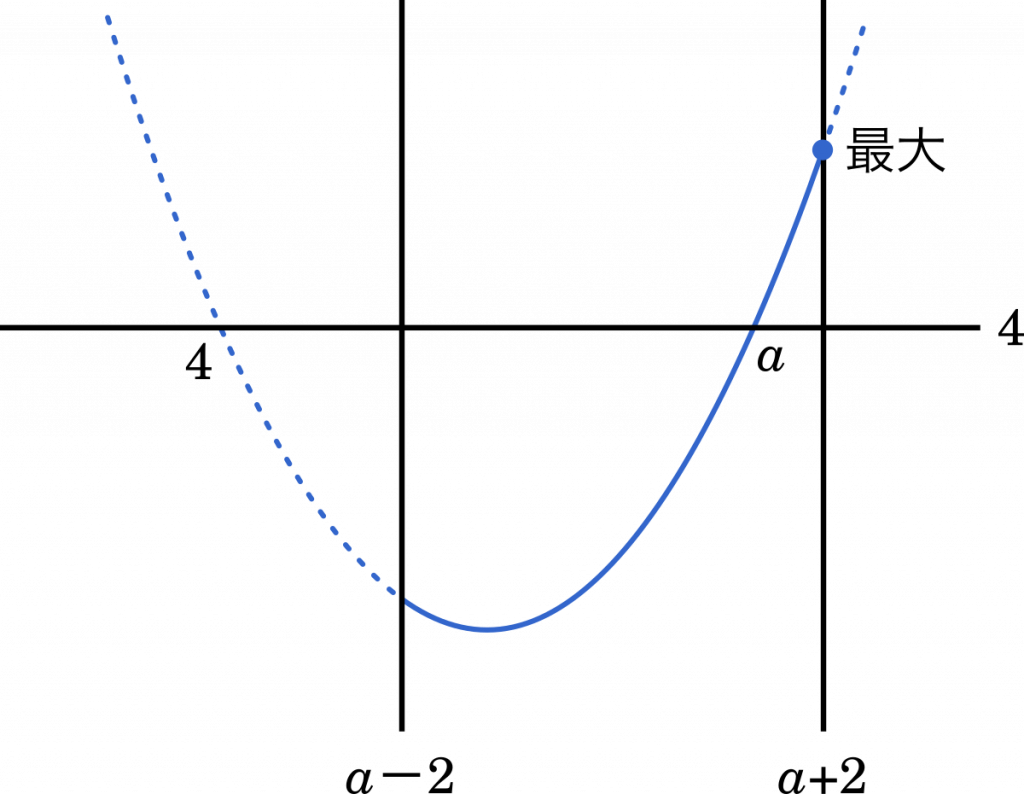
このように,$f(x)=4$ の直線を引くと,それぞれの値の位置関係がつかみやすくなる。
したがって,最大値は
$f(a+2)=(a+2-a)(a+2-4)+4$
$=2(a-2)+4$
$=2a-4+4$
$=2a$
・・・ネ
また,最小値を考えると
(i) $a-2\leqq\cfrac{a+4}{2}$ のとき
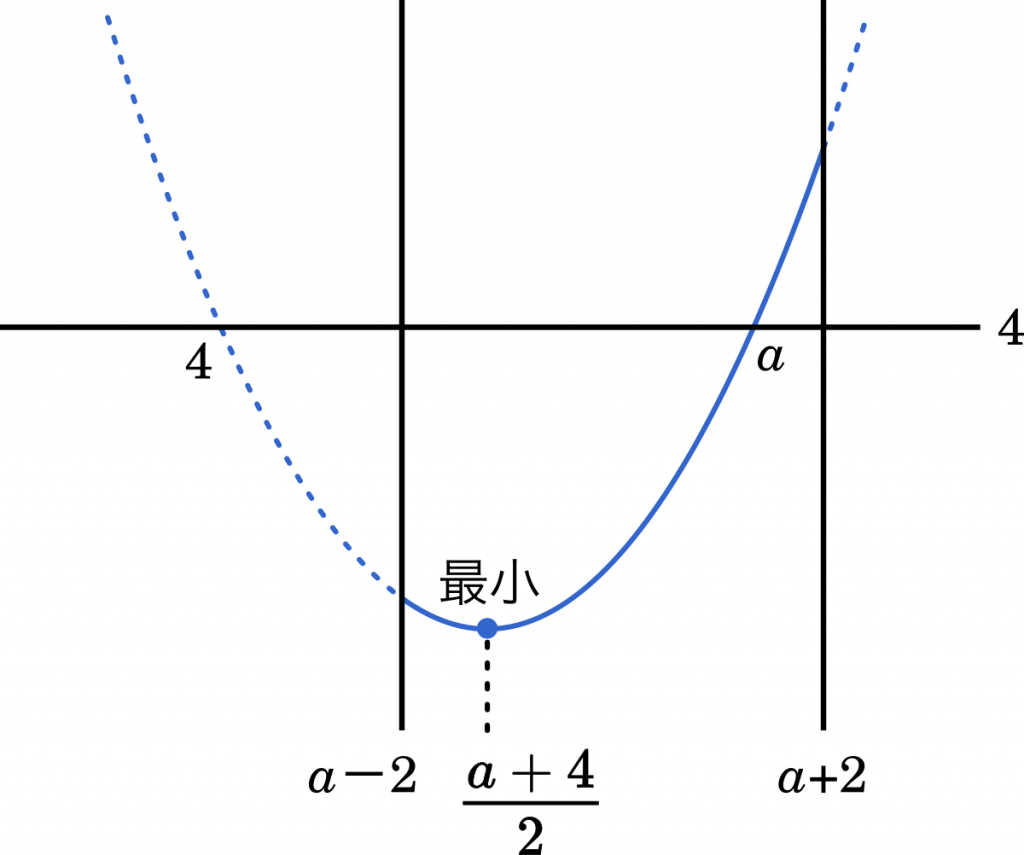
不等式を変形して
$2a-4\leqq a+4$
$a\leqq 8$
$a$ は 4 以上の定数だから
$4\leqq a\leqq8$
・・・ノ
最小値は $x=\cfrac{a+4}{2}$ のとき
$\cfrac{-1}{4}a^2+2a$
(ii) $8<a$ のとき
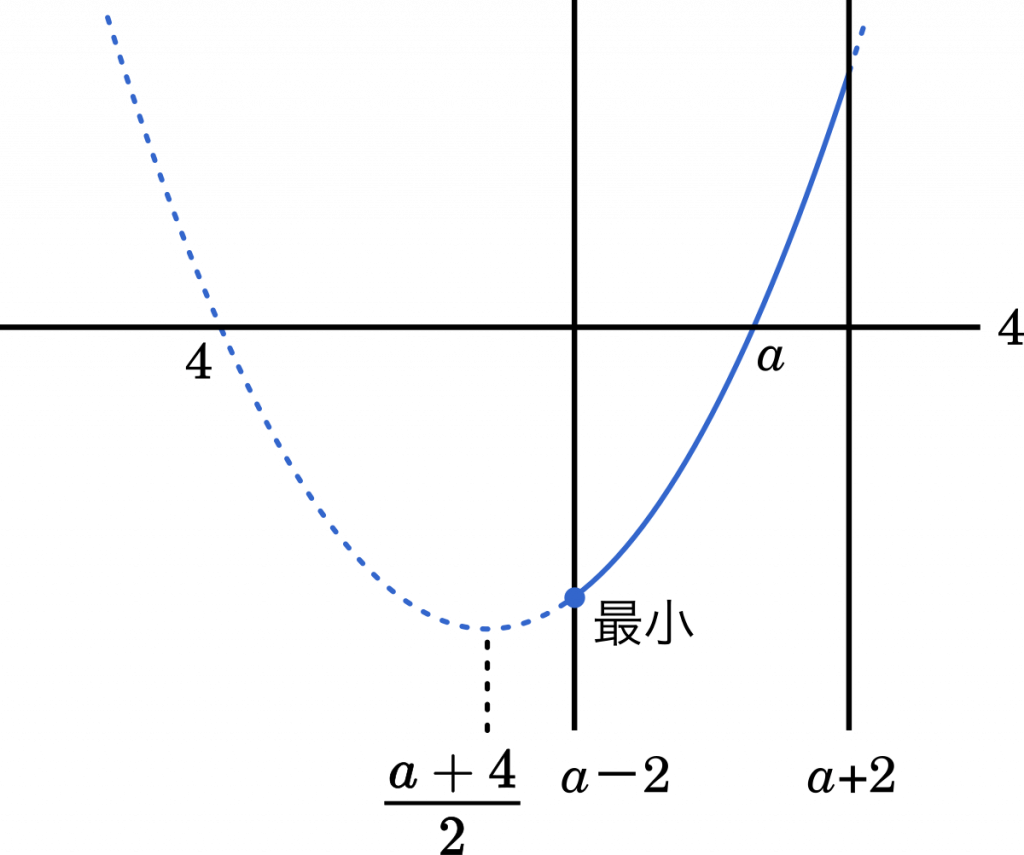
最小値は,$x=a^2$ のとき
$f(a-2)=(a-2-a)(a-2-4)+4$
$=-2(a-6)+4$
$=-2a+12+4$
$=-2a+16$
・・・ハヒフヘ
問題文
〔1〕$(19+5\sqrt{13})(19-5\sqrt{3})=\boxed{\text{アイ}}$ であるから,$19-5\sqrt{13}$ は正の実数である。$19+5\sqrt{13}$ の正の平方根を $\alpha$ とし,$19-5\sqrt{13}$ の正の平方根を $\beta$ とする。このとき
$\alpha^2+\beta^2=\boxed{\text{ウエ}}$,$\alpha\beta=\boxed{\text{オ}}$
であり
$(\alpha+\beta)^2=\boxed{\text{カキ}}$,$(\alpha-\beta)^2=\boxed{\text{クケ}}$
である。したがって
$\alpha=\cfrac{\boxed{\text{ コ }}\sqrt{\boxed{\text{ サ }}}+\sqrt{\boxed{\text{ シス }}}}{\boxed{\text{ セ }}}$
$\beta=\cfrac{\boxed{\text{ コ }}\sqrt{\boxed{\text{ サ }}}-\sqrt{\boxed{\text{ シス }}}}{\boxed{\text{ セ }}}$
〔2〕 $a$ を定数とする。実数 $x$ に関する二つの条件 $p,q$ を次のように定める。
$p:-1\leqq x\leqq3$
$q:|x-a|>3$
条件 $p,q$ の否定を $\bar{p},\bar{q}$ で表す。
(1) 命題「$p\implies q$」が真であるような $a$ の値の範囲は
$a<\boxed{\text{ ソタ }}$,$\boxed{\text{ チ }}< a$
である。
(2) $a=\boxed{\text{ チ }}$ のとき,$x=\boxed{\text{ ツ }}$ は命題「$p\implies q$」の反例である。
(3) 実数 $x$ に関する条件 $r$ を次のように定める。
$r:3 < x \leqq 4$
次の $\boxed{\text{ テ }}$ に当てはまるものを,下の⓪~③のうちから一つ選べ。
$\alpha=1$ のとき,条件「$\bar{p}$ かつ $\bar{q}$」は条件 $r$ であるための $\boxed{\text{ テ }}$。
⓪ 必要条件であるが,十分条件ではない
① 十分条件であるが,必要条件ではない
② 必要十分条件である
③ 必要条件でも十分条件でもない
〔3〕 $a$ を 4 以上の定数とし,$f(x)=(x-a)(x-4)+4$ とおく。
(1) 2 次関数 $y=f(x)$ の最小値は $\cfrac{\boxed{\text{ トナ }}}{\boxed{\text{ ニ }}}\space a^2+\boxed{\text{ ヌ }}\space a$ である。
(2) 2 次関数 $y=f(x)$ の $a-2\leqq x\leqq a+2$ における最大値は $\boxed{\text{ ネ }}\space a$ である。 また,2 次関数 $y=f(x)$ の $a-2\leqq x\leqq a+2$ における最小値は $4\leqq a\leqq \boxed{\text{ ノ }}$ のとき,$\cfrac{\boxed{\text{ トナ }}}{\boxed{\text{ ニ }}}\space a^2+\boxed{\text{ ヌ }}\space a$ であり,$\boxed{\text{ ノ }}< a$ のとき,$\boxed{\text{ ハヒ }}\space a+\boxed{\text{ フヘ }}$ である。
SNSでシェア