【数III複素数平面】z で表された式の絶対値の最大と最小を求める【国公立基本】
(1) 複素数平面上で等式
$$|3z-4i|=2|z-3i|$$
を満たす点 $z$ の全体はどのような図形を表すか答えなさい。
(2) 複素数 $z$ が(1)の等式を満たすとき,$\Big|z+\cfrac{1}{z}+2i\Big|$ の最大値と最小値を求めなさい。また,そのときの $z$ の値をそれぞれ求めなさい。(山口大2019)
2乗して絶対値を外す
(1)から進めます。

両辺を2乗すると
$|3z-4i|^2=4|z-3i|^2$
ここで,公式 $z\bar{z}=|z|^2$ を使います。
$(3z-4i)(\overline{3z-4i})=4(z-3i)(\overline{z-3i})$
$(3z-4i)(3\bar{z}+4i)=4(z-3i)(\bar{z}+3i)$
展開して
$9z\bar{z}+12iz-12i\bar{z}+16=4(z\bar{z}+3iz-3i\bar{z}+9)$
$9z\bar{z}+12iz-12i\bar{z}+16=4z\bar{z}+12iz-12i\bar{z}+36$
$5z\bar{z}-20=0$
$z\bar{z}=4$
$|z|^2=4$
$|z|=2$


したがって
原点を中心とする,半径 $2$ の円 (答え)
zをx+yiに置き換える
(2)に進みます。
絶対値の最大値と最小値を求めるのですが,$z$ は何らかの複素数を表しているだけなので,このままでは式がどのような値をとるのかさっぱり分かりません。そこで,$z$ を置きかえる必要があります。
置きかえ方は大きく分けると二通りあり,一つは極形式として表す方法,もう一つは $x,y$ を用いる方法です。
① 極形式 $z=r(\cos\theta+i\sin\theta)$
② 複素数 $z=x+yi$


今回は $x+yi$ で解いてみます。
$k^2=\Big(z+\cfrac{1}{z}+2i\Big)\Big(\overline{z+\cfrac{1}{z}+2i}\Big)$
$=\Big(z+\cfrac{1}{z}+2i\Big)\Big(\bar{z}+\cfrac{1}{\bar{z}}-2i\Big)$
$=z\bar{z}+\cfrac{z}{\bar{z}}-2iz+\cfrac{\bar{z}}{z}+\cfrac{1}{z\bar{z}}-\cfrac{2i}{z}+2i\bar{z}+\cfrac{2i}{\bar{z}}+4$
(1)より $z\bar{z}=4$ だから
$=4+\cfrac{z}{\bar{z}}-2iz+\cfrac{\bar{z}}{z}+\cfrac{1}{4}-\cfrac{2i}{z}+2i\bar{z}+\cfrac{2i}{\bar{z}}+4$
$=\cfrac{z^2+\bar{z}^2-2i\bar{z}+2iz}{z\bar{z}}+2i(\bar{z}-z)+8+\cfrac{1}{4}$
$=\cfrac{z^2+\bar{z}^2-2i\bar{z}+2iz}{4}+2i(\bar{z}-z)+8+\cfrac{1}{4}$
両辺を 4 倍して
$4k^2=z^2+\bar{z}^2-2i(\bar{z}-z)+8i(\bar{z}-z)+32+1$
$4k^2=z^2+\bar{z}^2+6i(\bar{z}-z)+33$
ここで
$(z+\bar{z})^2=z^2+2z\bar{z}+\bar{z}^2$
$=z^2+\bar{z}^2+8$
より
$z^2+\bar{z}^2=(z+\bar{z})^2-8$
だから
$4k^2=(z+\bar{z})^2+6i(\bar{z}-z)+25$
$z=x+yi,\bar{z}=x-yi$ とすると
$z+\bar{z}=x+yi+x-yi=2x$
$\bar{z}-z=x-yi-x-yi=-2yi$
となるので
$4k^2=(2x)^2+6i(-2yi)+25$
$=4x^2+12y+25$
また,$z$ は原点を中心とする半径 2 の円だから
$x^2+y^2=4$
$x^2=4-y^2$
が成り立つ。これを代入すると
$4k^2=4(4-y^2)+12y+25$
$=16-4y^2+12y+25$
$=-4y^2+12y+41$
これで,式が整理できました。あとはこの式の最大と最小を求めます。
式を平方完成すると
$4k^2=-4(y^2-3y)+41$
$=-4\Big(y-\cfrac{3}{2}\Big)^2+9+41$
$=-4\Big(y-\cfrac{3}{2}\Big)^2+50$
$x,y$ は原点を中心とする半径 2 の円周上の座標なので,$y$ の取り得る範囲は
$-2$ ≦ $y$ ≦ $2$
です。
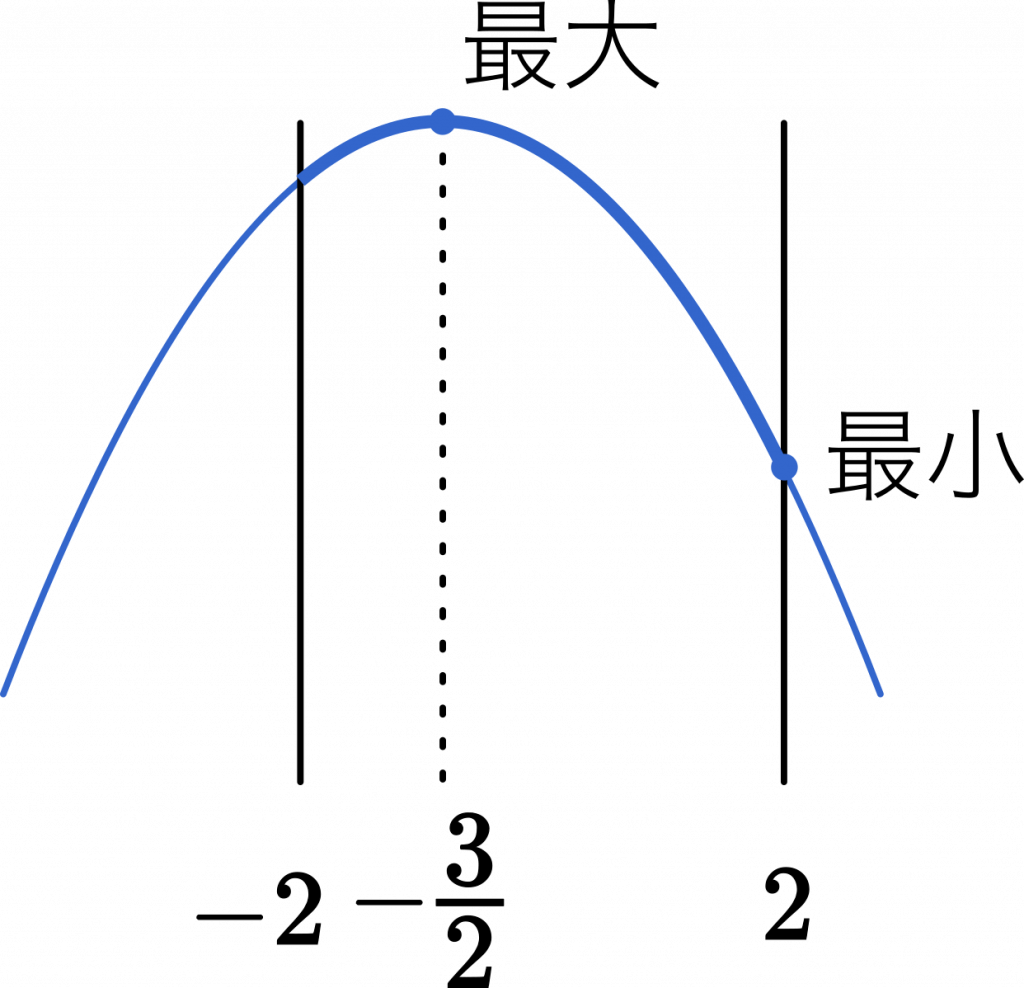
最大値は $y=-\cfrac{3}{2}$ のとき
$4k^2=50$
$k^2=\cfrac{25}{2}$
$k=\cfrac{5\sqrt{2}}{2}$
$z$ の値を求めると
$x^2+y^2=4$ より
$x^2+\cfrac{9}{4}=4$
$x^2=\cfrac{7}{4}$
$x=\pm\cfrac{\sqrt{7}}{2}$
よって
$z=\pm\cfrac{\sqrt{7}}{2}-\cfrac{3}{2}i$
また,最小値は $y=2$ のとき
$4k^2=-4\Big(2+\cfrac{3}{2}\Big)^2+50$
$4k^2=-49+50=1$
$k^2=\cfrac{1}{4}$
$k=\cfrac{1}{2}$
$z$ を求めると
$x^2+4=4$
$x^2=0$
$x=0$
よって
$z=-2i$
したがって
最大値は $z=\pm\cfrac{\sqrt{7}}{2}-\cfrac{3}{2}i$ のとき $\cfrac{5\sqrt{2}}{2}$
最小値は $z=-2i$ のとき $\cfrac{1}{2}$ (答え)
SNSでシェア