【数IA二次関数】格子点の個数を数える(千葉大)

放物線 $y=x^2$ と直線 $y=ax+b$ によって囲まれる領域を
$D=\{(x,y)|x^2\leqq y\leqq ax+b\}$
とし，$D$ の面積が $\cfrac{9}{2}$ であるとする。座標平面上で，$x$ 座標，$y$ 座標が共に整数である点を格子点と呼ぶ。(千葉大2010)

(1) $a=0$ のとき，$D$ に含まれる格子点の個数を求めよ。

(2) $a$，$b$ が共に整数であるとき，$D$ に含まれる格子点の個数は $a$，$b$ の値によらず一定であることを示せ。

式どうしを引く

$a=0$ のとき，直線の式は $y=b$ となります。格子点の数え方は，$x$ が $1$ のときに縦に～個，$x$ が $2$ のときに縦に～個，というように数えていくとよいでしょう。そのため，式どうしを引き算して，縦方向の距離が分かるようにします。

$f(x)=b-x^2$ とする。

ここで，放物線と直線の交点を求めておきます。

$x^2=b$ のとき
$x=\pm\sqrt{b}$

ここで面積 $\cfrac{9}{2}$ を利用しますが，２次関数と直線で６分の１公式というものがあったことを思いだしましょう。

よって

$S=\cfrac{1}{6}(\sqrt{b}+\sqrt{b})^3=\cfrac{(2\sqrt{b})^3}{6}=\cfrac{4b\sqrt{b}}{3}$

これが $\cfrac{9}{2}$ になるので

$\cfrac{4b\sqrt{b}}{3}=\cfrac{9}{2}$
$b\sqrt{b}=\cfrac{27}{8}$

$b\sqrt{b}=\sqrt{b^3}=b^{\small\frac{3}{2}}$ だから

$b^{\small\frac{3}{2}}=\Big(\cfrac{3}{2}\Big)^3$
$b^{\small\frac{1}{2}}=\cfrac{3}{2}$
$\sqrt{b}=\cfrac{3}{2}$

よって，交点の $x$ 座標は $\pm\cfrac{3}{2}$

また，$b=\cfrac{9}{4}$ より

$f(x)=\cfrac{9}{4}-x^2$

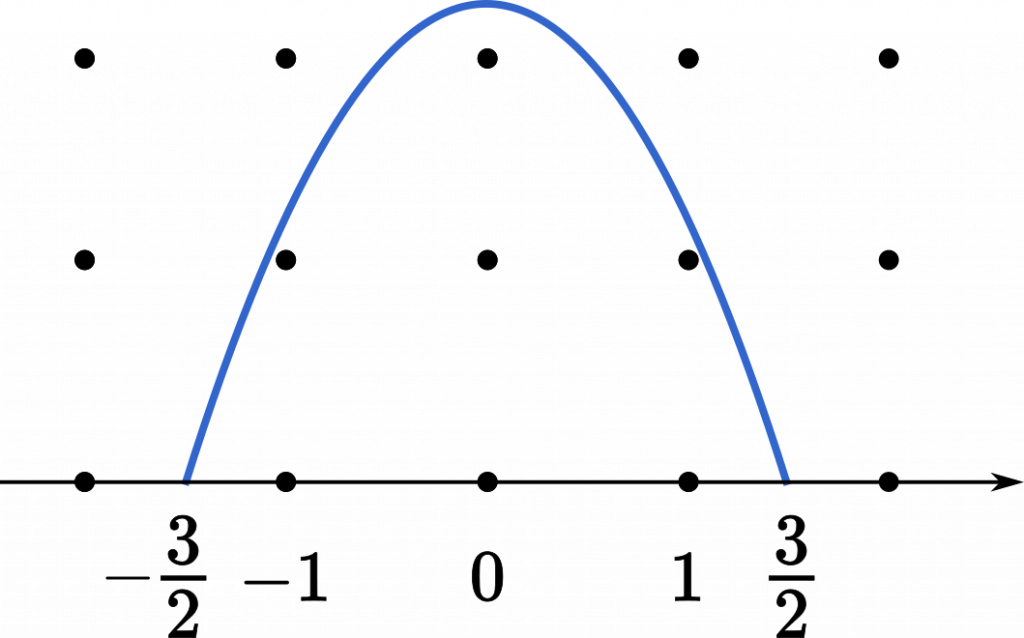
$f(-1)=\cfrac{9}{4}-1=\cfrac{5}{4}$

含まれる格子点の個数は２個。

$f(0)=\cfrac{9}{4}$
含まれる格子点の個数は３個。
$f(1)=\cfrac{9}{4}-1=\cfrac{5}{4}$
含まれる格子点の個数は２個。
したがって，
$2+3+2=7$ (個) (答え)

a,b が整数になる条件を考える

(2)に進みます。方針がつかみにくいですが，ともかく(1)と同じように式どうしを引き算して考えていきましょう。

$g(x)=ax+b-x^2$ とする。

放物線と直線の交点を求めると
$x^2=ax+b$
$x^2-ax-b=0$
$x=\cfrac{a\pm\sqrt{a^2+4b}}{2}$ ・・・①

６分の１公式を利用して
$S=\cfrac{1}{6}\Big(\cfrac{a+\sqrt{a^2+4b}}{2}-\cfrac{a-\sqrt{a^2+4b}}{2}\Big)^3$
$=\cfrac{1}{6}(\sqrt{a^2+4b})^3$

領域の面積は $\cfrac{9}{2}$ だったので
$\cfrac{1}{6}(a^2+4b)^{\small{\frac{3}{2}}}=\cfrac{9}{2}$
$(a^2+4b)^{\small{\frac{3}{2}}}=27$
$\sqrt{a^2+4b}=3$
$a^2+4b=9$
$4b=9-a^2$
$b=\cfrac{9-a^2}{4}$ ・・・②
①に代入して
$x=\cfrac{a\pm\sqrt{a^2+9-a^2}}{2}$
$=\cfrac{a\pm3}{2}$

これで，交点の座標が整理できました。

また，$b$ の値も分かったので $g(x)$ に戻して
$g(x)=-x^2+ax+\cfrac{9-a^2}{4}$
あとで計算がラクになるので平方完成しておきます。
$g(x)=-\Big(x-\cfrac{a}{2}\Big)^2+\cfrac{a^2}{4}+\cfrac{9-a^2}{4}$
$=-\Big(x-\cfrac{a}{2}\Big)^2+\cfrac{9}{4}$

ここから証明の方針を考えます。交点の一つである $\cfrac{a+3}{2}$ は $a$ が一つ増えると $\cfrac{1}{2}$ 増えることになります。つまり，$a$ の値によって $\cfrac{1}{2}$ ずつ平行移動していくイメージです。また，$a$ が偶数のときは 偶数＋３＝奇数となるので $\cfrac{a+3}{2}$ は分数になり，$a$ が奇数のときは 奇数＋３＝偶数となり，$\cfrac{a+3}{2}$ は整数になります。つまり，$a$ が奇数のときは交点は格子点を通ります。

(i) $a$ が偶数のとき
$k$ を整数として，$a=2k$ とすると
$b=\cfrac{9-4k^2}{4}$
$=\cfrac{9}{4}-k^2$
$b$ は整数なので，不適。

(ii) $a$ が奇数のとき
$a=2k+1$ とすると
$b=\cfrac{9-(2k+1)^2}{4}$
$=\cfrac{9-4k^2-4k-1}{4}$
$=\cfrac{-4k^2-4k+8}{4}$
$=-k^2-k+2$
条件を満たす整数 $b$ が存在する。
よって，$a$ は奇数であり，$\cfrac{a\pm3}{2}$ はともに整数である。

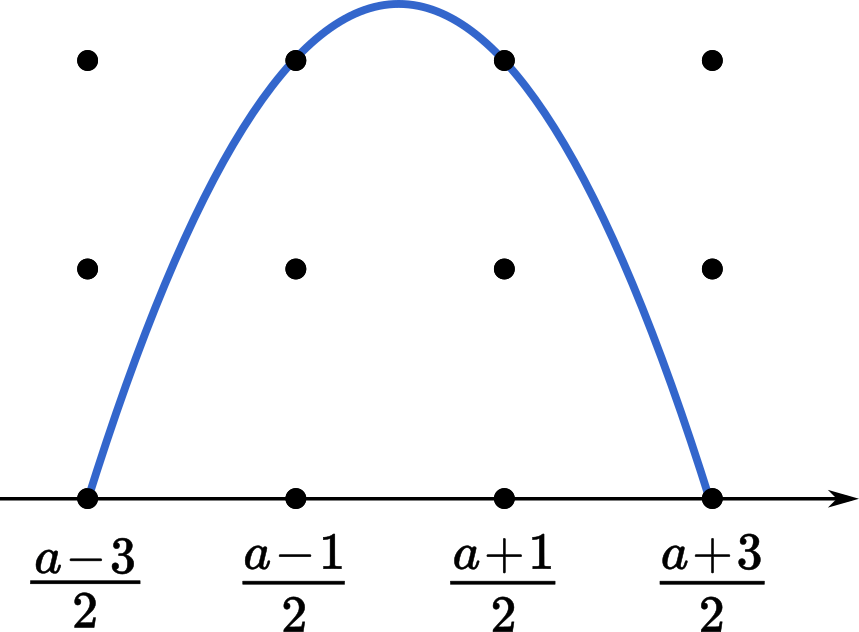
$g\Big(\cfrac{a-1}{2}\Big)=-\Big(\cfrac{a-1}{2}-\cfrac{a}{2}\Big)^2+\cfrac{9}{4}=2$
格子点の個数は３個
$g\Big(\cfrac{a+1}{2}\Big)=-\Big(\cfrac{a+1}{2}-\cfrac{a}{2}\Big)^2+\cfrac{9}{4}=2$
格子点の個数は３個
したがって，$D$ に含まれる格子点の個数は $a$，$b$ の値によらず
$1+3+3+1=8$ (個) である。(証明終わり)