【数学IA二次関数】格子点の個数を数える(千葉大2019第13問)

式どうしを引き算して数える

(1)から考えます。

まず $D(n)$ というのは，二つ目の不等式が
$y\leqq(2n+3)x-n(n+3)$
になる，という意味であることに注意します。

そして，$y=x^2$ を考えると，$x$ が整数なら $y$ も整数であり，また $y=(2n+3)x-n(n+3)$ も整数になります。

問題は２つの式にはさまれた領域に格子点が何個入るかです。これは縦方向に数えていけば分かります。

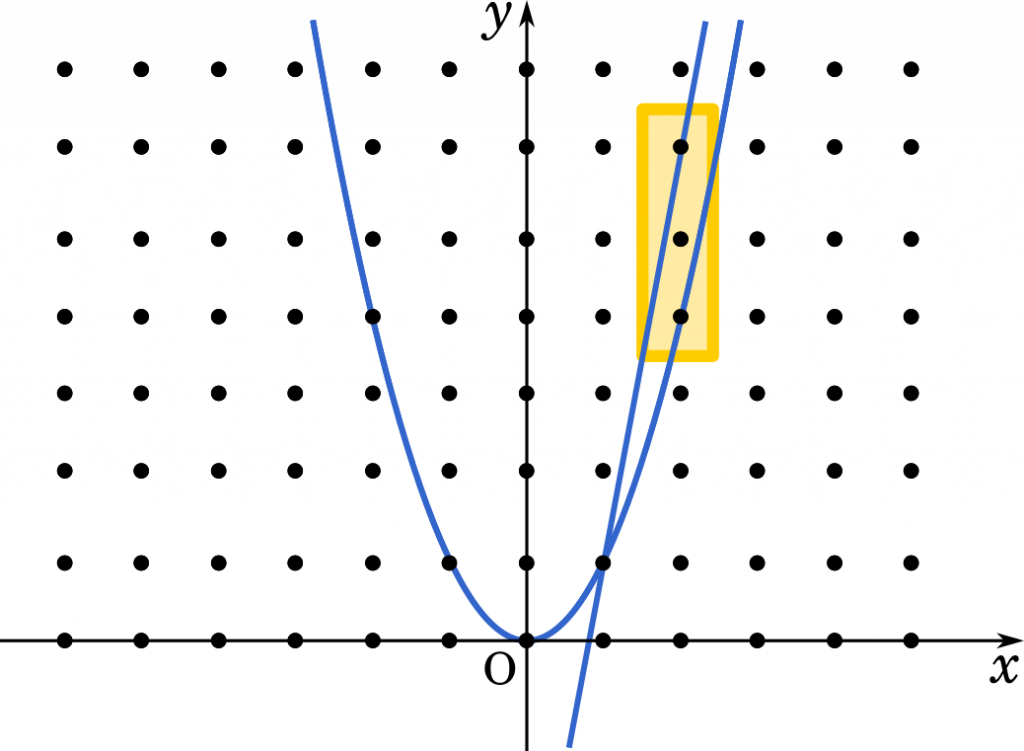
上の図は $n=1$ の場合ですが，$x=2$ のときを見ると，領域に含まれる格子点は３つあることが分かります。あとは，$x=4$ のとき，$x=5$ のとき・・・と順次数えていくことで全体の個数を数えることができます。
実際の個数は式の引き算によって求めます。たとえば $n=1$ で $x=2$ のとき
$y=x^2=4$
$y=(2\cdot1+3)\cdot2-1\cdot(1+3)=10-4=6$
引き算すると
$6-4=2$
ここで求められるのは２点間の距離だから，含まれる格子点の数は実際にはそれに１を加えた３個になることが分かります。
これをもとに，実際に式を作っていきましょう。
$y=x^2$ ・・・①
$y=(2a+3)x-a(a+3)$ ・・・②
$a=n$ として，①－②を $f(x)$ とすると
$f(x)=x^2-(2n+3)x-n(n+3)$
因数分解して
$=(x-n)(x-n-3)$
次に，①，②の交点を求めます。
$(x-n)(x-n-3)=0$ のとき
$x=n,n+3$
先ほど述べた通り，$x$ の値が整数のとき，$y$ の値は整数となるので，格子点を通ります。したがって，格子点の数はそれぞれ１個です。
あとは，$n$ と $n+3$ の間で数えていけばいいので
$x=n+1$ のとき
$f(n+1)=(n+1-n)(n+1-n-3)$
$=-2$
これは距離としては２ということなので，格子点の個数は３個です。
$x=n+2$ のとき
$f(n+2)=(n+2-n)(n+2-n-3)$
$=-2$
格子点の個数は３個。
したがって
$1+3+3+1=8$
格子点の個数は $8$ 個　(答え)

整数部分と小数部分に分けて考える

(2)に進みます。(1) で作った式を $a$ に戻して $f(x)=(x-a)(x-a-3)$ を使って考えていきましょう。

(1)より，$a$ が整数のとき，$D(a)$ に含まれる格子点の個数と $D(a+1)$ に含まれる格子点の個数は等しい。

問題は $a$ が整数でないときです。そこで $a$ を整数と小数部分に分けて考えていきます。

$a$ の整数部分を $s$，小数部分を $t$ とすると
$a=s+t$
$f(x)=(x-s-t)(x-s-t-3)$

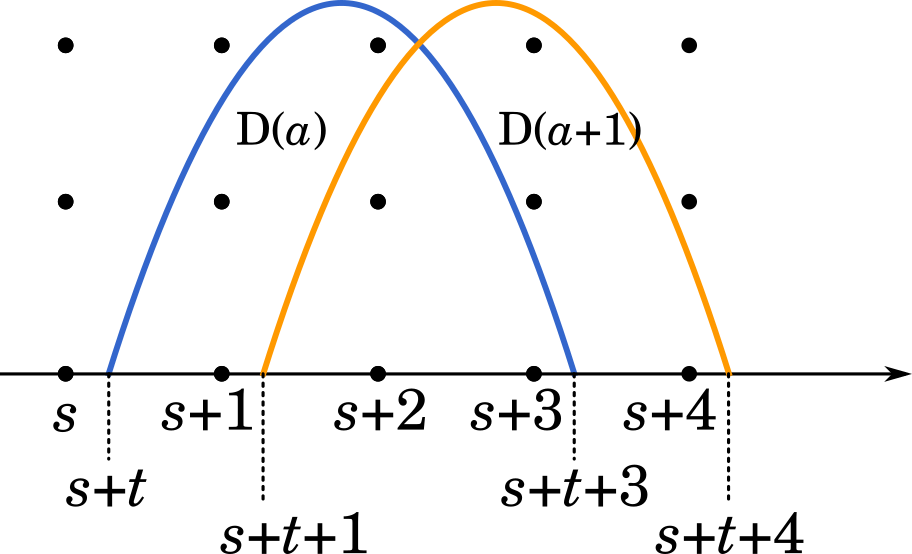
$f(x)$ をグラフに描いてみると上のようになります。結局，$a$ を $a+1$ に変えても領域と格子点は同様の位置関係になり，格子点の個数は同じであることが分かります。たとえば領域 $D(a)$ の $x=s+1$ のときと，$D(a+1)$ の $x=s+2$ において格子点の個数は同じです。

$D(a)$ のとき，$a=s+t$
$f(s+1)=(s+1-s-t)(s+1-s-t-3)$
$=(1-t)(-t-2)=-t-2+t^2+2t$
$=t^2+t-2$ ・・・③
$f(s+2)=(s+2-s-t)(s+2-s-t-3)$
$=t^2-t-2$ ・・・④
$f(s+3)=(s+3-s-t)(s+3-s-t-3)$
$=t^2-3t$ ・・・⑤

また

$D(a+1)$ のとき，$a+1=s+t+1$
$f(s+2)=(s+2-s-t-1)(s+2-s-t-4)$
$=(1-t)(-t-2)$
$=t^2＋t-2$ ・・・⑥
$f(s+3)=(s+3-s-t-1)(s+3-s-t-4)$
$=t^2-t-2$ ・・・⑦
$f(s+4)=(s+4-s-t-1)(s+4-s-t-4)$
$=t^2-3t$ ・・・⑧

③と⑥，④と⑦，⑤と⑧が同じ式になりました。

したがって，$D(a)$ に含まれる格子点の個数と $D(a+1)$ に含まれる格子点の個数は等しい。（証明終わり）