4次関数と極値－微分係数が 0 でも極値をもたない場合＆線形計画法と曲線(横浜国立大2016文系第2問)

実数 $a$，$b$ に対し，関数

$f(x)=x^4+2ax^3+(a^2+1)x^2-a^3+a+b$

がただ 1 つの極値をもち，その極値が 0 以上になるとする。次の問いに答えよ。

(1) $a$，$b$ のみたす条件を求めよ。

(2) $a$，$b$ が(1)の条件をみたすとき，$a-2b$ の最大値を求めよ。

微分係数が0でも極値であるとは限らない

(1)から始めます。

まず，式を微分して極値を考えてみます。

$f(x)=x^4+2ax^3+(a^2+1)x^2-a^3+a+b$
$f'(x)=4x^3+6ax^2+2(a^2+1)x$
$=2x(2x^2+3ax+a^2+1)$

$2x(2x^2+3ax+a^2+1)=0$ とすると

$x=0$

または

$2x^2+3ax+a^2+1=0$

よって，$x=0$ のときに微分係数が 0 になるのですが，だからと言って $f(x)$ が必ずしも極値をとるわけではありません。$x=0$ の前後で微分係数のプラス・マイナスが入れ替わるならば極値であると言えますが，符号が同じならば極値をとりません。

$2x(2x^2+3ax+a^2+1)$ について考えてみましょう。まず，$2x$ は $x=0$ の前後で符号が入れ替わります。そして，もし $2x^2+3ax+a^2+1$ が $x=0$ の前後で符号が変わらないならば，式全体としては，$x=0$ の前後で符号が入れ替わるといえます。

ある関数が $x=0$ の前後で符号が入れ替わるなら，その関数は原点を通過するはずです。

しかし，$2x^2+3ax+a^2+1$ に $x=0$ を代入すると $a^2+1$ となり，$a$ の値にかからわず正の値をとります。よって，原点を通過することはありません。

よって，$2x^2+3ax+a^2+1$ は $x=0$ の前後で符号が入れ替わることはなく，一方で $f'(x)$ は $x=0$ の前後で符号が入れ替わることになります。よって，$f(x)$ は $x=0$ のとき極値をもちます。

問題文から，極値は 0 以上だから

$f(0)=-a^3+a+b\geqq0$
$b\geqq a^3-a$

となります。

$f(x)$ はただ 1 つの極値をもつので，$x=0$ で極値をもつとき，$2x^2+3ax+a^2+1$ は解なしであると考えられます。ちなみに $x=0$ が解になることはありません。

$x=0$ を代入すると

$a^2+1=0$ ⇔ $a=i$ ($a$は実数より不適)

$2x^2+3ax+a^2+1$ が解をもたないとき，判別式を用いて

$D=9a^2-8a^2-8<0$
$a^2-8<0$
$(a+2\sqrt{2})(a-2\sqrt{2})<0$

よって $-2\sqrt{2}<a<2\sqrt{2}$

ここで，もう一つ見落としているものがあります。$2x^2+3ax+a^2+1$ が解をもつとしても，その前後で微分係数のプラス・マイナスが入れ替わらないならば，極値をもたないことになります。

$2x^2+3ax+a^2+1$ は 2 次関数だから，実数解を 2 つもつ場合，プラス・マイナスの入れ替わりが起こります。しかし，実数解が 1 つの場合には，符号は入れ替わりません。

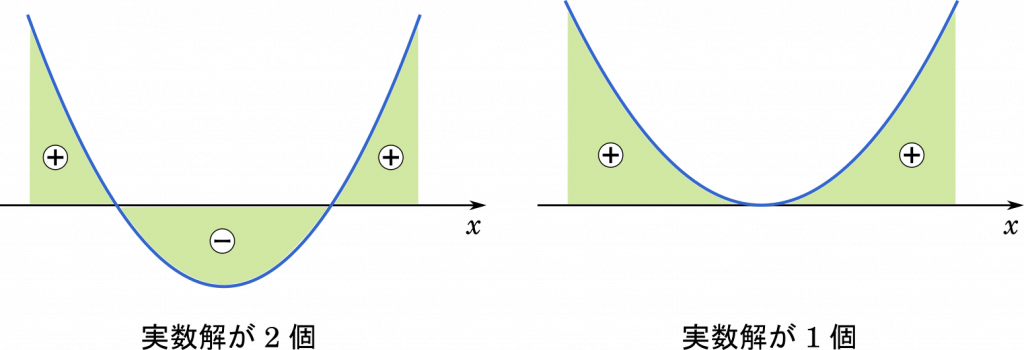
そこで，判別式を用いて実数解が 1 個の場合を検討しましょう。

$D=9a^2-8a^2-8=0$

$a^2-8=0$
$a=\pm2\sqrt{2}$

つまり，$a=\pm2\sqrt{2}$ のとき，$f'(x)$ は $x=0$ 以外にも解をもち，微分係数が 0 になるのですが，それは極値にはならないので，$f(x)$ は $x=0$ でただ 1 つの極値をもつことになります。

したがって，$a$，$b$ のみたす条件は

$-2\sqrt{2}\leqq a\leqq2\sqrt{2}$
$b\geqq a^3-a$

（答え）

a，b のグラフをつくって考える

(2)に進みます。

(1) で $a$，$b$ の条件が分かったので，まずは $a$ を横軸，$b$ を縦軸としたグラフを描いてみましょう。

$g(a)=a^3-a$ とすると

$g'(a)=3a^2-1$

$3a^2-1=0$ とすると

$a=\pm\cfrac{1}{3}$

増減表は

$\def\arraystretch{1.5}\begin{array}{|c|c|c|c|c|c|c|c|c|c|}\hline a&-2\sqrt{2}&\cdots&-\frac{1}{3}&\cdots&0&\cdots&\frac{1}{3}&\cdots&2\sqrt{2}\\\hline g'(a)&&+&0&-&-&-&0&+\\\hline g(a)&-14\sqrt{2}&\nearrow&\frac{8}{27}&\searrow&0&\searrow&-\frac{8}{27}&\nearrow&14\sqrt{2}\\\hline\end{array}$

$g(-2\sqrt{2})=(-2\sqrt{2})^3-(-2\sqrt{2})=-14\sqrt{2}$

$g\Big(-\cfrac{1}{3}\Big)=\Big(-\cfrac{1}{3}\Big)^3-\Big(-\cfrac{1}{3}\Big)=\cfrac{8}{27}$

$g(0)=0$

$g\Big(\cfrac{1}{3}\Big)=\Big(\cfrac{1}{3}\Big)^3-\Big(\cfrac{1}{3}\Big)=-\cfrac{8}{27}$

$g(2\sqrt{2})=(2\sqrt{2})^3-2\sqrt{2}=14\sqrt{2}$

次に $a-2b=k$ とすると

$b=\cfrac{a}{2}-\cfrac{k}{2}$

となります。これは，$a$ の 1 次関数であり，$-\cfrac{k}{2}$ が切片となります。

あとは，直線が領域を通過しつつ，$-\cfrac{k}{2}$ がもっとも小さくなる場合を考えれば $k$ の最大が求められます。

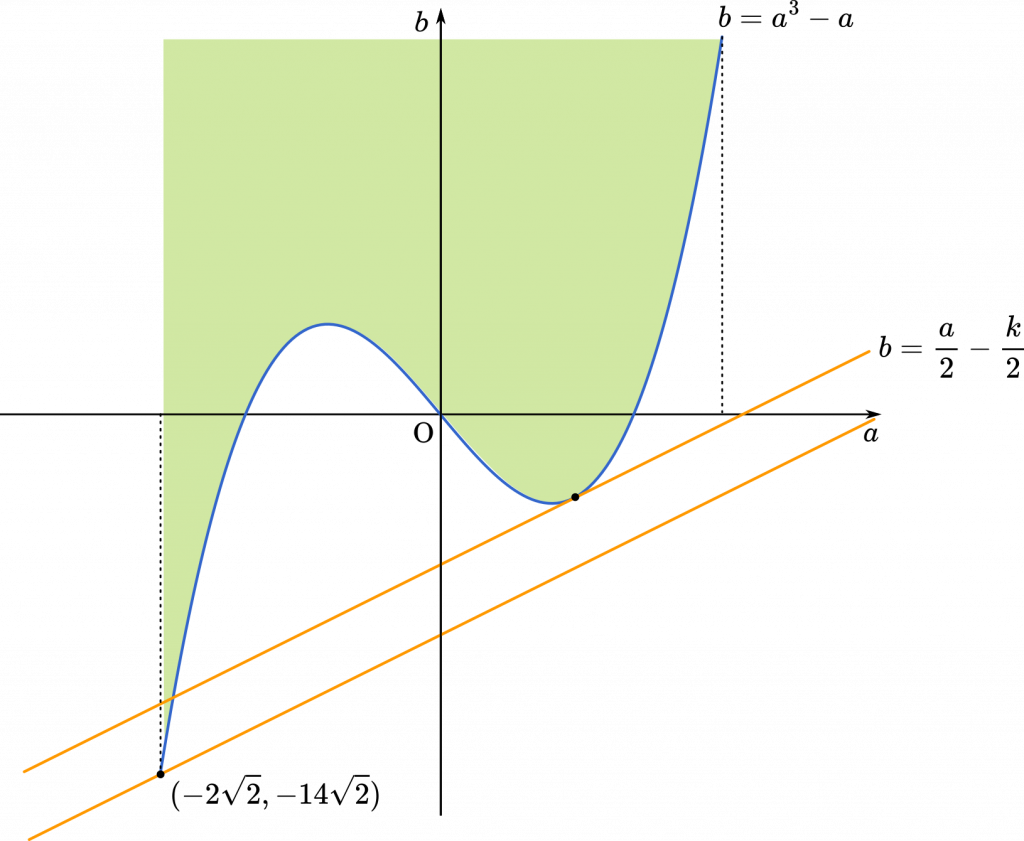
直線をタテ方向に並行移動していくと，$k$ の値が最小になりそうな点が 2 点あることがわかります。実際に試験問題を解いているときには，グラフはあくまでおおまかなものしか描けないので，実際にどちらの方が $k$ の値が小さくなるかは計算で求めていくことになります。

(i) 直線が $(a,b)=(-2\sqrt{2},-14\sqrt{2})$ を通るとき

$k=a-2b$
$=-2\sqrt{2}-2(-14\sqrt{2})$
$=26\sqrt{2}$

(ii) $b=a^3-a$ と $b=\cfrac{a}{2}-\cfrac{k}{2}$ が $0<a<2\sqrt{2}$ の範囲で 1 点で交わるとき

直線の傾きは $\cfrac{1}{2}$ だから，曲線の微分係数も $\cfrac{1}{2}$ です。

$3a^2-1=\cfrac{1}{2}$ とすると

$3a^2=\cfrac{3}{2}$

$a>0$ より

$a=\cfrac{\sqrt{2}}{2}$

$g\Big(\cfrac{\sqrt{2}}{2}\Big)=\Big(\cfrac{\sqrt{2}}{2}\Big)^3-\cfrac{\sqrt{2}}{2}$
$=-\cfrac{\sqrt{2}}{4}$

つまり直線と曲線は $(a,b)=\Big(\cfrac{\sqrt{2}}{2},-\cfrac{\sqrt{2}}{4}\Big)$ で接することになります。

これを代入して $k$ の値を求めましょう。

$k=\cfrac{\sqrt{2}}{2}-2\Big(-\cfrac{\sqrt{2}}{4}\Big)=\sqrt{2}$

$26\sqrt{2}$ と $\sqrt{2}$ を比べれば $26\sqrt{2}$ の方が大きいのは明らかです。

したがって

$a-2b$ の最大値は $26\sqrt{2}$　（答え）