４次関数の変曲点と接線の交点：変曲点で重解をとるイメージの捉え方(神戸大2015理系第3問)

$a$ を正の実数とする。座標平面上の曲線 $C$ を

$y=x^4-2(a+1)x^3+3ax^2$

で定める。曲線 $C$ が 2 つの変曲点 P，Q をもち，それらの $x$ 座標の差が $\sqrt{2}$ であるとする。以下の問に答えよ。

(1) $a$ の値を求めよ。

(2) 線分 PQ の中点と $x$ 座標が一致するような，$C$ 上の点を R とする。三角形 PQR の面積を求めよ。

(3) 曲線 $C$ 上の点 P における接線が P 以外で $C$ と交わる点を P’ とし，点 Q における接線が Q 以外で $C$ と交わる点を Q’ とする。線分 P’Q’ の中点の $x$ 座標を求めよ。

第二次導関数を求める

(1)から始めます。

変曲点の $x$ 座標について考えていきましょう。

$y=x^4-2(a+1)x^3+3ax^2$  より
$y’=4x^3-6(a+1)x^2+6ax$
$y”=12x^2-12(a+1)x+6a$

$12x^2-12(a+1)x+6a=0$ とすると
$2x^2-2(a+1)x+a=0$

$x=\cfrac{a+1\pm\sqrt{(a+1)^2-2a}}{2}$
$=\cfrac{a+1\pm\sqrt{a^2+2a+1-2a}}{2}$
$=\cfrac{a+1\pm\sqrt{a^2+1}}{2}$　・・・①

解の差は $\sqrt{2}$ だから

$\cfrac{a+1+\sqrt{a^2+1}}{2}-\cfrac{a+1-\sqrt{a^2+1}}{2}=\sqrt{2}$
$\sqrt{a^2+1}=\sqrt{2}$

両辺を 2 乗して

$a^2+1=2$
$a^2=1$

$a$ は正の実数だから

$a=1$　（答え）

三角形の面積

(2)に進みます。

PQ の中点を M とすると次のようになります。

この問題の解き方は一通りではないのですが，ここでは素直に点 M の座標を求めて面積を求めてみます。

まず，$a=1$ を代入して

$y=x^4-2(1+1)x^3+3\cdot1\cdot x^2$
$=x^4-4x^3+3x^2$

また

$y”=12x^2-12(1+1)x+6a$
$=12x^2-24x+6$

$12x^2-24x+6=0$ とすると
$2x^2-4x+1=0$

方程式の解を $\alpha,\beta$ とすると，中点 M の $x$ 座標は $\cfrac{\alpha+\beta}{2}$ だから，解と係数の関係より

$\alpha+\beta=-\Big(-\cfrac{4}{2}\Big)=2$
$\cfrac{\alpha+\beta}{2}=1$

これで，点 M の $x$ 座標が 1 であることが分かりました。また

$x=1$ のとき

$y=1^4-4\cdot1^3+3\cdot1^2=0$

点 R の座標は R$(1,0)$

次に，点 M の $y$ 座標を求めていきます。

点 M の $y$ 座標を求めると

$\cfrac{1}{2}(\alpha^4-4\alpha^3+3\alpha^2+\beta^4-4\beta^3+3\beta^2)$
$=\cfrac{1}{2}\{\alpha^4+\beta^4-4(\alpha^3+\beta^3)+3(\alpha^2+\beta^2)\}$　・・・②

① に $a=1$ を代入すると

$x=\cfrac{1+1\pm\sqrt{1^2+1}}{2}$
$x=\cfrac{2\pm\sqrt{2}}{2}$

$\alpha=\cfrac{2-\sqrt{2}}{2}$，$\beta=\cfrac{2+\sqrt{2}}{2}$

よって

$\alpha+\beta=\cfrac{2-\sqrt{2}}{2}+\cfrac{2+\sqrt{2}}{2}=2$
$\alpha\beta=\cfrac{2-\sqrt{2}}{2}\cdot\cfrac{2+\sqrt{2}}{2}$
$=\cfrac{(2-\sqrt{2})(2+\sqrt{2})}{4}$
$=\cfrac{4-2}{2}=\cfrac{1}{2}$

これらを利用して $\alpha^4+\beta^4$ まで求めていきましょう。

$\alpha^2+\beta^2=(\alpha+\beta)^2-2\alpha\beta$
$=2^2-2\cdot\cfrac{1}{2}=3$

$\alpha^3+\beta^3=(\alpha+\beta)(\alpha^2-\alpha\beta+\beta^2)$
$=2\cdot\Big(3-\cfrac{1}{2}\Big)$
$=2\cdot\cfrac{5}{2}=5$

$\alpha^4+\beta^4=(\alpha^2+\beta^2)^2-2(\alpha\beta)^2$
$=3^2-2\cdot\Big(\cfrac{1}{2}\Big)^2$
$=9-\cfrac{1}{2}=\cfrac{17}{2}$

これらを②に代入すると

$\cfrac{1}{2}\Big(\cfrac{17}{2}-4\cdot5+3\cdot3\Big)$
$=\cfrac{1}{2}\Big(-\cfrac{5}{2}\Big)=-\cfrac{5}{4}$

ここから，RM の長さは $\cfrac{5}{4}$ であることが分かります。

したがって面積は

$S=\cfrac{1}{2}\cdot\sqrt{2}\cdot\cfrac{5}{4}$
$=\cfrac{5\sqrt{2}}{8}$　（答え）

変曲点と接線の性質

(3)に進みます。

変曲点から接線をひくと，次のようになります。

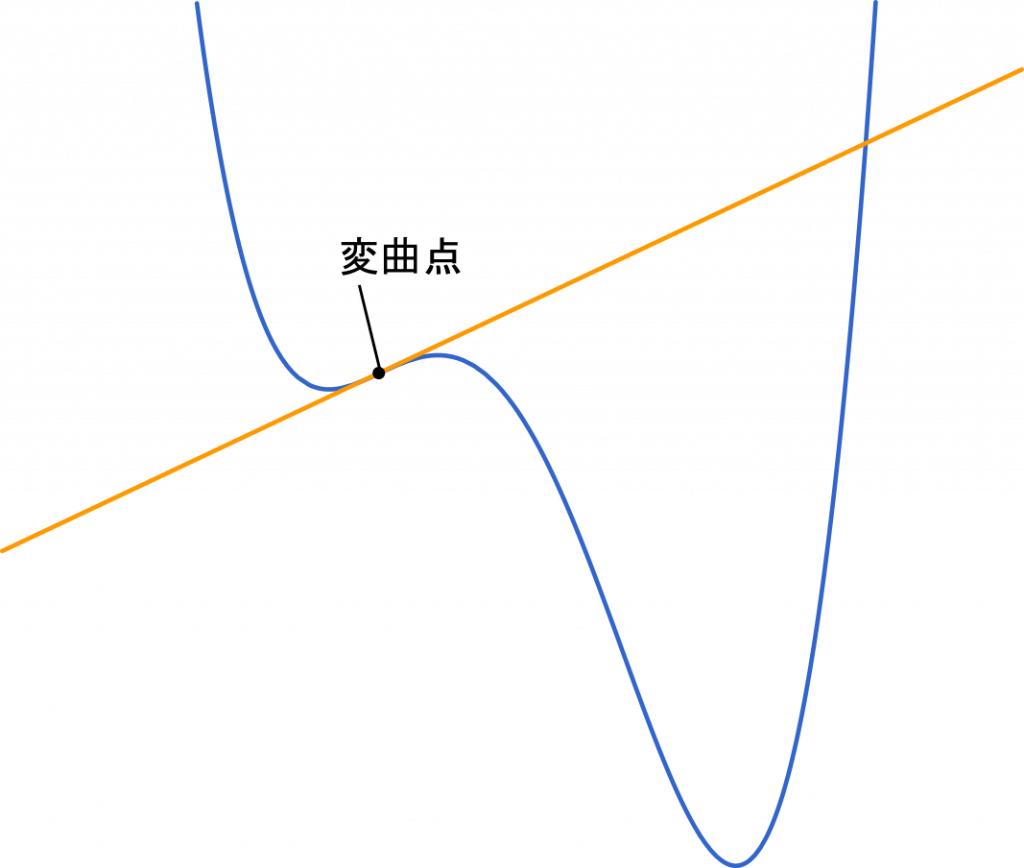
こうしてみると，曲線と直線は共有点を 2 個もつことが分かります。

接線の方程式をつくりましょう。

点 P の座標を $(\alpha,\alpha^4-4\alpha^3+3\alpha^2)$ とすると

$y’=4x^3-12x^2+6x$ より

$y=(4\alpha^3-12\alpha^2+6\alpha)(x-\alpha)+\alpha^4-4\alpha^3+3\alpha^2$
$=(4\alpha^3-12\alpha^2+6\alpha)x-4\alpha^4+12\alpha^3-6\alpha^2+\alpha^4-4\alpha^3+3\alpha^2$
$=(4\alpha^3-12\alpha^2+6\alpha)x-3\alpha^4+8\alpha^3-3\alpha^2$

$C$ と連立すると

$x^4-4x^3+3x^2=(4\alpha^3-12\alpha^2+6\alpha)x-3\alpha^4+8\alpha^3-3\alpha^2$
$x^4-4x^3+3x^2-(4\alpha^3-12\alpha^2+6\alpha)x+3\alpha^4-8\alpha^3+3\alpha^2=0$

これは 4 次方程式だから，解は 4 個できるはずです。しかし，上で述べたように実際の解は 2 個です。つまり，重解をとります。

そして，解のうち 3 個が変曲点に集まります。

イメージとしてはこのような感じです。

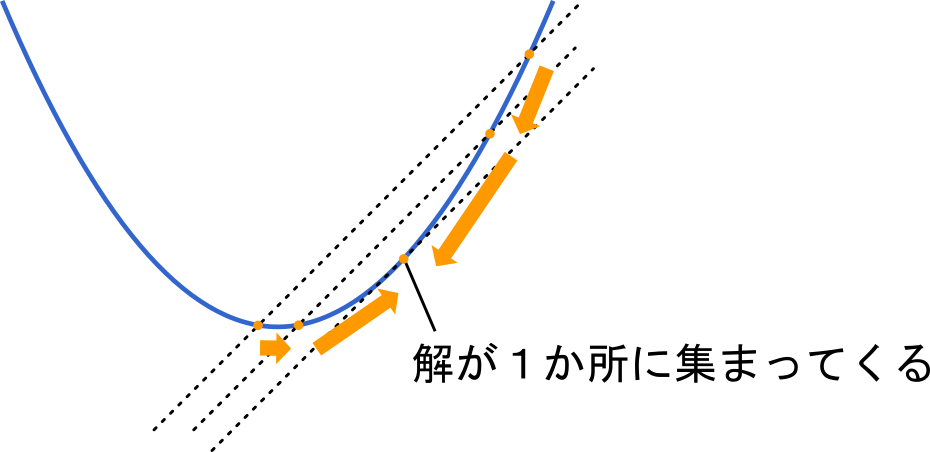
曲線と直線を引いてみます。そして，直線が接線となる位置まで移動していくと，2 個あった交点が最終的に 1 個の点に集まっていくことが分かると思います。これが重解です。

あくまでイメージですが，変曲点の場合も複数ある交点が変曲点に近づくにつれて 1 か所に集まってくると考えると良いでしょう。

方程式は，$x=\alpha$ を解にもつので

$x^4-4x^3+3x^2-(4\alpha^3-12\alpha^2+6\alpha)x+3\alpha^4-8\alpha^3+3\alpha^2=0$

組立除法を用いて

$\begin{matrix}1&-4&3&-4\alpha^3+12\alpha^2-6\alpha&3\alpha^4-8\alpha^3+3\alpha^2&|\underline{\alpha}\\&\alpha&\alpha^2-4\alpha&\alpha^3-4\alpha^2+3\alpha&-3\alpha^4+8\alpha^3-3\alpha^2\\\hline1&\alpha-4&\alpha^2-4\alpha+3&-3\alpha^3+8\alpha^2-3\alpha&0\end{matrix}$

$(x-\alpha)\{x^3+(\alpha-4)x^2+(\alpha^2-4\alpha+3)x-3\alpha^3+8\alpha^2-3\alpha\}=0$

$\begin{matrix}1&\alpha-4&\alpha^2-4\alpha+3&-3\alpha^3+8\alpha^2-3\alpha&|\underline{\alpha}\\&\alpha&2\alpha^2-4\alpha&3\alpha^3-8\alpha^2+3\alpha\\\hline1&2\alpha-4&3\alpha^2-8\alpha+3&0\end{matrix}$

$(x-\alpha)^2\{x^2+(2\alpha-4)x+3\alpha^2-8\alpha+3\}=0$

$\begin{matrix}\end{matrix}$

$\begin{matrix}1&2\alpha-4&3\alpha^2-8\alpha+3&|\underline{\alpha}\\&\alpha&3\alpha^2-4\alpha\\\hline1&3\alpha-4&6\alpha^2-12\alpha+3\end{matrix}$

ここで，(2)より $y”=2x^2-4x+1=0$ でした，これに $\alpha$ を代入して

$2\alpha^2-4\alpha+1=0$
$6\alpha^2-12\alpha+3=0$

となるので

$(x-\alpha)^3(x+3\alpha-4)=0$

よって，P’ の $x$ 座標は $4-3\alpha$

同様にして，Q’ の $x$ 座標は $4-3\beta$

中点は $\cfrac{4-3\alpha+4-3\beta}{2}$

$=\cfrac{8-3(\alpha+\beta)}{2}$
$=4-\cfrac{3}{2}(\alpha+\beta)$

(2)より $\alpha+\beta=2$ だから

$=1$　（答え）