3 次方程式の解の 1 つが分かっているとき式が因数分解できることを利用する問題(横浜国立大2018理系第5問)

$xy$ 平面上に双曲線 $C_1:y=\cfrac{1}{x}$ がある。$C_1$ 上の点 P$\Big(t,\cfrac{1}{t}\Big)$ $(t>0)$ における $C_1$ の接線を $\ell$ とする。放物線 $C_2:y=x^2+ax+b$ ($a,b$ は実数)は点 P を通り，$C_1$ と第 3 象限において共有点をただ 1 つもつとする。$C_2$ と $\ell$ で囲まれた部分の面積を $S$ とする。次の問いに答えよ。

(1) $\ell$ の方程式を求めよ。

(2) $a,b$ をそれぞれ $t$ の式で表せ。

(3) $S$ を $t$ の式で表せ。

(4) $t$ が正の実数全体を動くとき，$S$ の最小値を求めよ。

接線の方程式

(1)から始めます。まずは，グラフの概形を描いておきましょう。

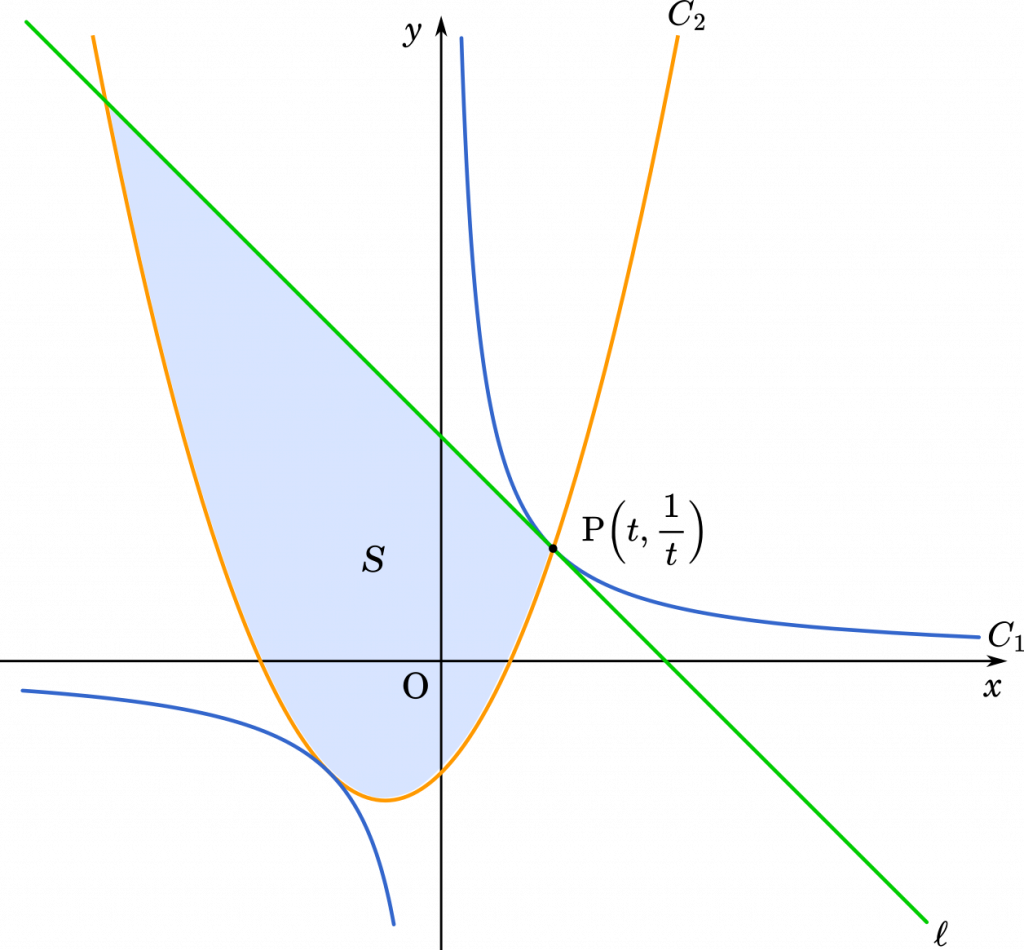
$\ell$ は接線なので，$C_1$ を微分して接線の傾きを求めましょう。

$y=\cfrac{1}{x}=x^{-1}$
$y’=-x^{-2}$
$=-\cfrac{1}{x^2}$

$\ell$ は $\Big(t,\cfrac{1}{t}\Big)$ を通る，傾き $-\cfrac{1}{t^2}$ の直線だから

$\ell:y-\cfrac{1}{t}=-\cfrac{1}{t^2}(x-t)$
$y=-\cfrac{1}{t^2}x+\cfrac{1}{t}+\cfrac{1}{t}$
$=-\cfrac{1}{t^2}x+\cfrac{2}{t}$　（答え）

式を因数分解する

(2)に進みます。

$a,b$ を求めていきますが，$y=x^2+ax+b$ だけでは手がかりがありません。こういうときは，問題文の条件から何らかの式を作ってみることが大切です。

$C_1$ と $C_2$ は共有点をもつので，式を連立すると

$\cfrac{1}{x}=x^2+ax+b$　・・・①
$x^3+ax^2+bx-1=0$　・・・②

$C_1$ と $C_2$ は $x=t$ で共有点を持つので，$x=t$ は方程式の解の一つである。よって

$t^3+at^2+bt-1=0$ ・・・③

$C_1$ と $C_2$ は第 3 象限でも共有点を 1 つもつので，それが分かれば何らかの式が作れそうなのですが，もちろん分かりません。

この問題は解き方が一通りではないのですが，ここではなるべく教科書の基本的な知識に基づいて解いていきます。

数IIで高次方程式を習っていたときに，因数定理というものがあったことを思い出せれば突破口が見えてきます。

これは言い換えると，方程式の解の一つが $x=t$ であるとき，その方程式は $x-t$ で割り切れるということです。

これを使って，実際に方程式を割ってみましょう。

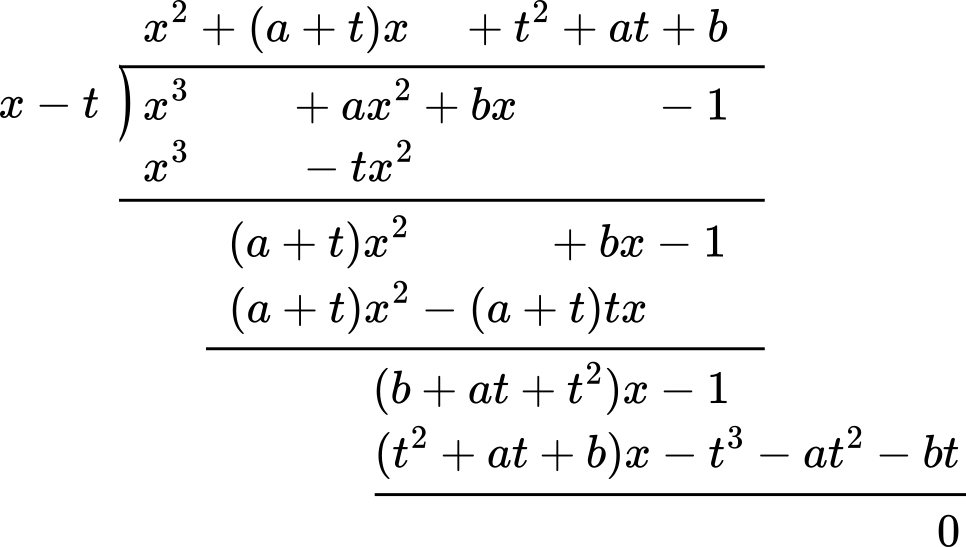
よって，②は

$(x-t)\{x^2+(a+t)x+t^2+at+b\}=0$

と因数分解できる。これより

$x^2+(a+t)x+t^2+at+b=0$　・・・④

ここで，一つテクニックです。①を $x=t$ とすると

$\cfrac{1}{t}=t^2+at+b$　・・・⑤

となるので，④に代入すると

$x^2+(a+t)x+\cfrac{1}{t}=0$　・・・⑥

この方法は，必ず使わないと解けないというわけではないのですが，使った方が計算上ラクになります。

この方程式の解は，第 3 象限の共有点の $x$ 座標になります。そして，共有点は 1 つなので，判別式 $D=0$ になります。

$D=(a+t)^2-\cfrac{4}{t}=0$
$a^2+2at+t^2-\cfrac{4}{t}=0$

これで，$a$ の値が求められそうです。

$a^2+2ta+t^2-\cfrac{4}{t}=0$ とすると，式は $a$ の二次方程式となるので

$a=-t\pm\sqrt{t^2-t^2+\cfrac{4}{t}}$
$=-t\pm\sqrt{\cfrac{4}{t}}$
$=-t\pm\cfrac{2}{\sqrt{t}}$

共有点の $x$ 座標は負の値になるので

・$a=-t+\cfrac{2}{\sqrt{t}}$ のとき

⑥に代入すると

$x^2+\cfrac{2}{\sqrt{t}}x+\cfrac{1}{t}=0$

$x=-\cfrac{1}{\sqrt{t}}$　（$t>0$より，負の値）

・$a=-t-\cfrac{2}{\sqrt{t}}$ のとき
$x^2-\cfrac{2}{\sqrt{t}}x+\cfrac{1}{t}=0$
$x=\cfrac{1}{\sqrt{t}}$　（正の値）

よって

$a=\cfrac{2}{\sqrt{t}}-t$

これを，⑤に代入すると

$\cfrac{1}{t}=t^2+\Big(\cfrac{2}{\sqrt{t}}-t\Big)t+b$
$\cfrac{1}{t}=t^2+2\sqrt{t}-t^2+b$
$b=\cfrac{1}{t}-2\sqrt{t}$

したがって

$(a,b)=\Big(\cfrac{2}{\sqrt{t}}-t,\space\cfrac{1}{t}-2\sqrt{t}\Big)$　（答え）

6分の1公式で面積を求める

(3)に進みます。

$\ell:y=-\cfrac{1}{t^2}x+\cfrac{2}{t}$
$C_2:y=x^2+ax+b$
$=x^2+\Big(\cfrac{2}{\sqrt{t}}-t\Big)x+\cfrac{1}{t}-2\sqrt{t}$

二次関数と直線がつくる面積なので，ここは 6 分の 1 公式を使いましょう。

式を連立すると

$x^2+\Big(\cfrac{2}{\sqrt{t}}-t+\cfrac{1}{t^2}\Big)x+\cfrac{1}{t}-2\sqrt{t}-\cfrac{2}{t}=0$
$x^2+\Big(\cfrac{2}{\sqrt{t}}-t+\cfrac{1}{t^2}\Big)x-\cfrac{1}{t}-2\sqrt{t}=0$

解と係数の関係より

$\alpha+\beta=-\cfrac{2}{\sqrt{t}}+t-\cfrac{1}{t^2}$

ここで，$\beta$ は点 P のことだから，$\beta=t$ である。よって

$\alpha=-\cfrac{2}{\sqrt{t}}-\cfrac{1}{t^2}$

$\beta-\alpha=t+\cfrac{2}{\sqrt{t}}+\cfrac{1}{t^2}$
$=t+\cfrac{2\sqrt{t}}{t}+\cfrac{1}{t^2}$
$=(\sqrt{t})^2+\cfrac{2\sqrt{t}}{t}+\cfrac{1}{t^2}$
$=\Big(\sqrt{t}+\cfrac{1}{t}\Big)^2$

したがって

$S=\cfrac{1}{6}\Big(\sqrt{t}+\cfrac{1}{t}\Big)^3$　（答え）

最小値を求める

(4)に進みます。

$S=\cfrac{1}{6}\Big(\sqrt{t}+\cfrac{1}{t}\Big)^3$ より，$\sqrt{t}+\cfrac{1}{t}$ の最小値を求めれば良さそうです。

$f(t)=\sqrt{t}+\cfrac{1}{t}$　として

$=t^{\small{\frac{1}{2}}}+t^{-1}$

$f'(t)=\cfrac{1}{2}t^{\small{-\frac{1}{2}}}-t^{-2}$
$=\cfrac{1}{2\sqrt{t}}-\cfrac{1}{t^2}$

$\cfrac{1}{2\sqrt{t}}-\cfrac{1}{t^2}=0$ とすると

$\cfrac{1}{2\sqrt{t}}=\cfrac{1}{t^2}$
$\cfrac{t^2}{\sqrt{t}}=2$
$\cfrac{t^4}{t}=4$
$t^3=4$
$t=\sqrt[3]{4}$

$\def\arraystretch{1.5}\begin{array}{|c|c|c|c|}\hline t&\cdots&\sqrt[3]{4}&\cdots\\\hline f'(t)&-&0&+\\\hline f(t)&\searrow&&\nearrow\\\hline\end{array}$

$f(\sqrt[3]{4})=\sqrt{\sqrt[3]{4}}+\cfrac{1}{\sqrt[3]{4}}$

指数になおして，式を整理していきます。

$=(4^{\small{\frac{1}{3}}})^{\small{\frac{1}{2}}}+4^{\small{-\frac{1}{3}}}$
$=4^{\small{\frac{1}{6}}}+4^{\small{-\frac{2}{6}}}$
$=4^{\small{\frac{1}{6}}}+4^{\small{\frac{1}{6}-\frac{3}{6}}}$
$=4^{\small{\frac{1}{6}}}(1+4^{\small{-\frac{3}{6}}})$
$=4^{\small{\frac{1}{6}}}(1+4^{\small{-\frac{1}{2}}})$
$=4^{\small{\frac{1}{6}}}\Big(1+\cfrac{1}{\sqrt{4}}\Big)$
$=4^{\small{\frac{1}{6}}}\Big(1+\cfrac{1}{2}\Big)$
$=4^{\small{\frac{1}{6}}}\cdot\cfrac{3}{2}$

したがって

$S=\cfrac{1}{6}\Big(4^{\small{\frac{1}{6}}}\cdot\cfrac{3}{2}\Big)^6$
$S=\cfrac{1}{6}\cdot4^{\small{\frac{1}{6}\times6}}\cdot\Big(\cfrac{3}{2}\Big)^6$
$=\cfrac{4}{6}\cdot\cfrac{3^6}{2^6}$
$=\cfrac{2}{3}\cdot\cfrac{3^6}{2^6}$
$=\cfrac{3^5}{2^5}$
$=\cfrac{243}{32}$　（答え）