【意外とやっかい】1/sin x の積分のやりかた(横浜国立大2017理系第1問)
次の問いに答えよ。
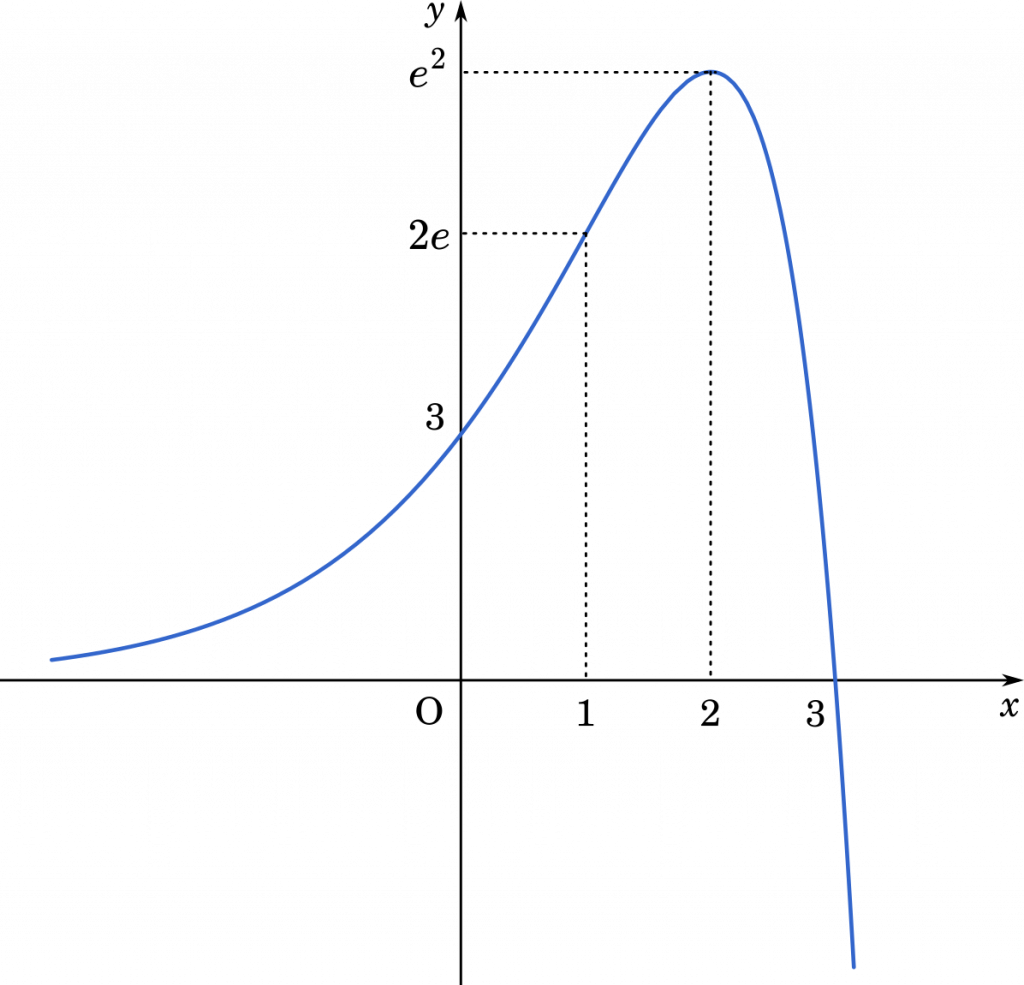
(1) 関数 $f(x)=(3-x)e^x$ について,関数の増減,極値,グラフの凹凸を調べ,$y=f(x)$ のグラフの概形をかけ。ただし,$\displaystyle\lim_{x\rightarrow\infty}\cfrac{x}{e^x}=0$ は証明なしで用いてよい。
(2) 定積分
$\displaystyle\int_0^{\small{\frac{\pi}{2}}}\cfrac{dx}{3\sin x+4\cos x}$
を求めよ。
第二次導関数を求める
(1)から始めます。
問題文のような聞かれ方をしたときには,第二次導関数を求めます。
積の微分の公式を用いて
$f'(x)=(3-x)’e^x+(3-x)(e^x)’$
$=-e^x+(3-x)e^x$
$=e^x(-1+3-x)$
$=e^x(2-x)$
極値を求めておきます。
$e^x(2-x)=0$ として
$e^x\not=0$ だから
$2-x=0$
$x=2$
次に第二次導関数を求めます。
$f”(x)=(e^x)'(2-x)+e^x(2-x)’$
$=e^x(2-x)-e^x$
$=e^x(2-x-1)$
$=e^x(1-x)$
$e^x(1-x)=0$ として
$e^x\not=0$ だから
$x=1$
| $x$ | $(-\infty)$ | $\cdots$ | $1$ | $\cdots$ | $2$ | $\cdots$ | $(\infty)$ |
| $f'(x)$ | + | + | + | 0 | $-$ | ||
| $f”(x)$ | + | 0 | $-$ | $-$ | $-$ | ||
| $f(x)$ | 0 | $2e$ | $e^2$ | $(-\infty)$ |
$f(1)=2e$
$f(2)=e^2$
また
$f(-x)=(3+x)e^{-x}$
$=3e^{-x}+xe^{-x}$
$=\cfrac{3}{e^x}+\cfrac{x}{e^t}$
となるので
$\displaystyle\lim_{x\rightarrow-\infty}f(-x)$
$=0+0=0$
また
$\displaystyle\lim_{x\rightarrow\infty}f(x)$
$=\displaystyle\lim_{x\rightarrow\infty}(3-x)e^x$
$=-\infty$
1/sin x の積分
(2)に進みます。
$\displaystyle\int_0^{\small{\frac{\pi}{2}}}\cfrac{dx}{3\sin x+4\cos x}$
まずは分母を三角関数の合成でまとめましょう。
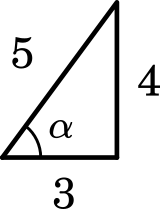
$3\sin x+4\cos x=5\sin(x+\alpha)$
ただし $\sin\alpha=\cfrac{4}{5}$,$\cos\alpha=\cfrac{3}{5}$

よって
$=\cfrac{1}{5}\displaystyle\int_0^{\small{\frac{\pi}{2}}}\cfrac{dx}{\sin(x+\alpha)}$
ここから,置換積分をしておきます。
$x+\alpha=t$ とすると
$dx=dt$
$\def\arraystretch{1.5}\begin{array}{|c|c|}\hline x&0\rightarrow\frac{\pi}{2}\\\hline t&\alpha\rightarrow\frac{\pi}{2}+\alpha\\\hline\end{array}$
よって
$=\cfrac{1}{5}\displaystyle\int_\alpha^{\small{\frac{\pi}{2}+\alpha}}\cfrac{dt}{\sin t}$


$\cfrac{1}{\sin x}$ を変形すると
$=\cfrac{\sin x}{\sin^2x}$
$=\cfrac{\sin x}{1-\cos^2x}$
$=\cfrac{\sin x}{(1+\cos x)(1-\cos x)}$
これを部分分数分解します。
$\cfrac{1}{1+\cos x}+\cfrac{1}{1-\cos x}$
$=\cfrac{1-\cos x+1+\cos x}{(1+\cos x)(1-\cos x)}$
$=\cfrac{2}{(1+\cos x)(1-\cos x)}$
となることを利用する。


$\cfrac{\sin x}{(1+\cos x)(1-\cos x)}$
$=\cfrac{1}{2}\Big(\cfrac{\sin x}{1+\cos x}+\cfrac{\sin x}{1-\cos x}\Big)$
これを用いて
$\cfrac{1}{5}\displaystyle\int_\alpha^{\small{\frac{\pi}{2}+\alpha}}\cfrac{dt}{\sin t}$
$\cfrac{1}{10}\displaystyle\int_\alpha^{\small{\frac{\pi}{2}+\alpha}}\Big(\cfrac{\sin t}{1+\cos t}+\cfrac{\sin t}{1-\cos t}\Big)\space dt$
$=\cfrac{1}{10}\Big[-\log(1+\cos t)+\log(1-\cos t)\Big]_\alpha^{\small{\frac{\pi}{2}+\alpha}}$
$=\cfrac{1}{10}\Big[\log\cfrac{1-\cos t}{1+\cos t}\Big]_\alpha^{\small{\frac{\pi}{2}+\alpha}}$
ここで,$\cos\Big(\cfrac{\pi}{2}+\alpha\Big)=-\sin\alpha=-\cfrac{4}{5}$

公式として暗記しても良いのですが,単位円を書いて解決する方が現実的でしょう。
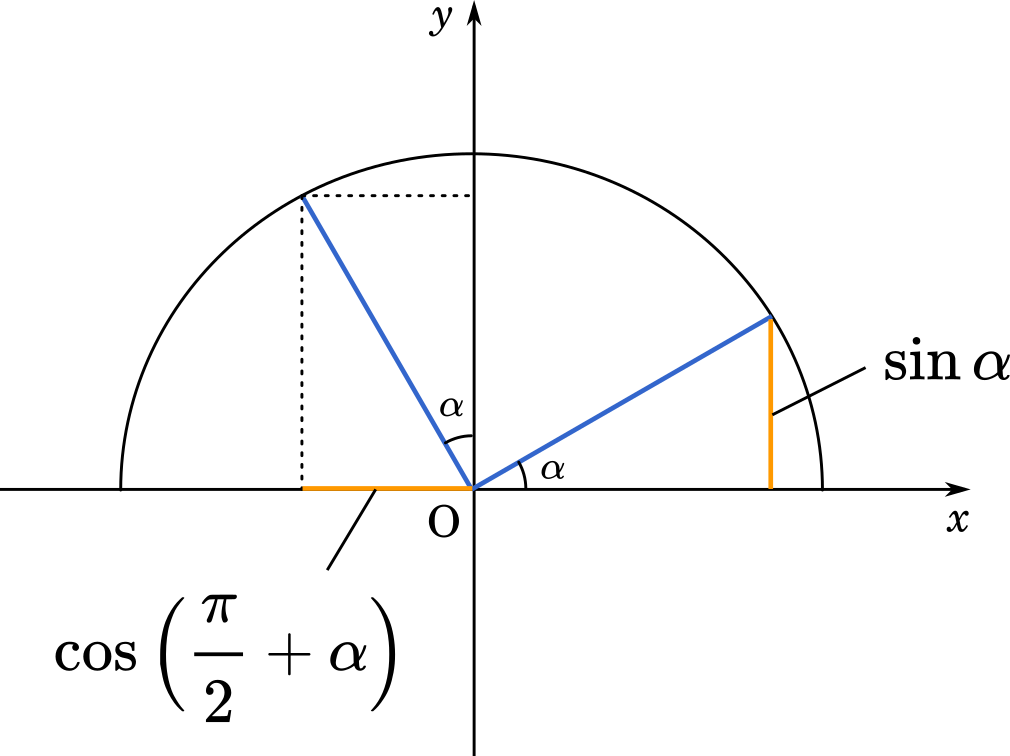
このように単位円を書いてみると,第2象限の $\cos\Big(\cfrac{\pi}{2}+\alpha\Big)$ は第1象限の $\sin\alpha$ と同じ大きさです。ただし,第2象限の $\cos$ は負の値なので,$\cos\Big(\cfrac{\pi}{2}+\alpha\Big)=-\sin\alpha$ とします。
$=\cfrac{1}{10}\left(\log\cfrac{1+\cfrac{4}{5}}{1-\cfrac{4}{5}}-\log\cfrac{1-\cfrac{3}{5}}{1+\cfrac{3}{5}}\right)$
$=\cfrac{1}{10}\Big(\log\cfrac{9}{1}-\log\cfrac{2}{8}\Big)$
$=\cfrac{1}{10}\Big(\log9-\log\cfrac{1}{4}\Big)$
$=\cfrac{1}{10}(\log9-\log1+\log4)$
$=\cfrac{1}{10}\log36$
$=\cfrac{1}{10}\log6^2$
$=\cfrac{1}{5}\log6$ (答え)
SNSでシェア